[Admin]

in reply to: Quadratic Factors #8117

Fully factorise 4x⁴ – 13x² + 9.

4 × 9 = 36: -9, – 4 will multiply to 36 and add to -13

= 4x⁴ – 4x² – 9x² + 9

= 4x²(x² – 1) – 9(x² – 1)

= (x² – 1)(4x² – 9)

= (x – 1)(x + 1)(2x – 3)(2x + 3)

[Admin]

in reply to: Trig Maxima/Minima #7653

A sector has a radius r cm and contains an angle θ radians. The area of the sector is 100 cm².
a. Show that perimeter P cm of the sector is given by $$P= 2r +\frac{ 200}{r}$$.
b. If r and θ vary in such a way that the area of the sector remains constant at 100 cm², find the values of r and θ which give the least value of P.

a. A = ½r²θ = 100
r²θ = 200
$$\theta=\frac{200}{r^2}$$

P = arc length + r + r   where L = θr
$$P = \theta\times r+ 2r$$

$$P=\frac{200}{r^2}\times r+ 2r$$

$$P =\frac{200}{r}+2r$$

 

b.  P = 200r^-1 + 2r

P’ = -200r^-2 + 2

P”= 400r^-3

P’ = $$\frac{-200}{r^2}+2=0$$

$$\frac{-200}{r^2}=-2$$

-200 = -2r²

100 = r²

r = ±10

consider r = 10 (as we can’t have negative gradients)

when r = 10

P”=$$\frac{400}{10^3}>0$$

∴ concave up, hence minimum

 

when r = 0

$$\theta=\frac{200}{10^2}$$

θ = 2

∴ minimum when r = 10 and θ = 2

 

[Admin]

in reply to: Tax #7267

Using the tax table below, calculate the taxable income if $25,416 was paid in tax.

TAXABLE INCOME	TAX
$1 – $8,000	Nil	Nil
$8,001 – $23,600	Nil	16c for each $1 in excess of $8,000
$23,601 – $65,000	$2,496	30c for each $1 in excess of $23,600
$65,001 – $97,000	$14,916	42c for each $1 in excess of $65,000
$97,001 and over	$28,356	48c for each $1 in excess of $97,000

Find the tax bracket, which will have to be the $65,001 – $97,000, as the one below is too high.

25,416 = 14,916 + 0.42(x – 65,000)               ^{subtract 14,916 from both sides}

10,500 = 0.42(x – 65,000)               ^{divide both sides by 0.42}

25,000 = x – 65,000               ^{tadd 65,000 to both sides}

x = 90,000

∴ Taxable Income was $90,000

[Admin]

in reply to: Arc lengths, Sectors & Segments #906

A sector of a circle with radius 5cm and an angle of  subtended at the centre is cut out of cardboard. It is then curved around to form a cone. Find its exact surface area and volume.
the arc length will form the circumference of the cone, and the radius will form the slant height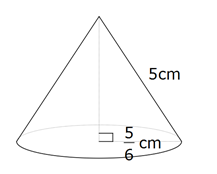

ℓ = $$5 \times \frac{\pi }{3}$$

C = $$\frac{{5\pi }}{3} = 2\pi r$$

r = ⁵/₆

h² = 5² – (⁵/₆)²

h² = $$\frac{{875}}{{36}}$$

h = $$\frac{{5\sqrt {35} }}{6}$$

$$V = \frac{1}{3}\pi  \times {\left( {\frac{5}{6}} \right)^2} \times \frac{{5\sqrt {35} }}{6}$$

$$V = \frac{{125\sqrt {35} \pi }}{{648}}cm^3$$

$$SA=\pi\,r^2+\pi\,r\,l$$  where L is the slant height

$$SA = \pi  \times {\left( {\frac{5}{6}} \right)^2} + \pi  \times \frac{5}{6} \times 5$$

$$=\frac{{175\pi }}{{36}}cm^2$$ 

[Admin]

in reply to: AP: Tn #708

The 2nd term of an arithmetic sequence is 13 and the 5th term is 31. What is the 17th term of this sequence?

T_n = a + (n – 1)d

T₂ = 13 = a + d

T₅ = 31 = a + 4d

subtracting them:

-18 = -3d
d = 6
13 = a + 6
a = 7

T₁₇ = 7 + (17 – 1)6

= 103

[Admin]

in reply to: Motion #605

A particle moves along the x-axis with an acceleration given by a = 6t + 3. When t = 0, x = 5 and the velocity of the particle is 1 unit per second. Find the position of the particle after 3 seconds.

v = $$\frac{{6{t^2}}}{2} + 3t + c$$

v = 3t² + 3t + c

when t = 0, v = 11 = 3(0)² + 3(0) + c

c = 1 v = 3t² + 3t + 1

x = $$\frac{{3{t^3}}}{3} + \frac{{3{t^2}}}{2} + t + k$$

x = $${t^3} + \frac{{3{t^2}}}{2} + t + k$$

when t = 0, x = 5

5 = 0 + 0 + 0 + k k = 5

∴ $$x = {t^3} + \frac{{3{t^2}}}{2} + t + 5$$

when t = 3

x = 27 + ²⁷/2 + 3 + 5

= 48.5

Attachments:

You must be logged in to view attached files.

[Admin]

in reply to: Relationship between Roots and Coefficients #535

One root of the equation x² – 6x + c = 0 is twice the other root. Find the value of c.

let α = 2β

α + β = –^-6/₁

α + β = 6

2β + β = 6

3β = 6

β = 2

αβ = ^c/₁

2β× β = c

2 × 2 × 2 = c

c = 8

[Admin]

in reply to: Relationship between Roots and Coefficients #534

3x² + kx + 4 = 0 : one root is three times the other. Find the 2 possible values of k.

let β = 3α

α +β = –^k/₃

α + 3α = –^k/₃

4α = –^k/₃

α = –^k/₁₂

αβ = ⁴/₃

3α² = ⁴/₃

3( –^k/₁₂)² = ⁴/₃

$$\frac{3k^2}{144} =\frac{4}{3}$$

k² = 64

k = ±8

[Admin]

in reply to: Relationship between Roots and Coefficients #15708

Consider P(x) = x³ – 3x – k.

a. If P(0) < 0 and P(2) > 0 show that 0 < k < 2.

b. If k = 1 show that the equation P(x) = 0 has three real roots.

a. P(0) < 0 then
x³ – 3(0) – k < 0
-k < 0 k > 0
and
P(2) > 0 then
2³ – 3(2) – k > 0
8 – 6 – k > 0
-k > -2
k < 2
hence 0 < k < 2

b. x³ – 3x – 1 = 0
easiest way to prove this is with calculus

y’ = 3x² – 3 = 0
y’ = 3(x² – 1) = 0
3(x – 1)(x + 1) = 0
x = -1 and x = 1
(-1, 1) and (1, -4)
since a cubic with one turning point above the x-axis and one turning point below the x-axis
there must be three roots

(a cubic can have 1 root: both turning points above or below the x-axis
2 roots: one turning point on the x-axis and one either above or below the x-axis
3 roots: one above and one below the x-axis)

[Author]

Posts