Forum Replies Created
-
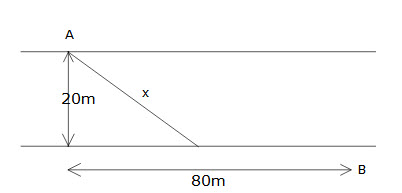Grant is at point A on one side of a 20m wide river and needs to get to point B on the other side 80 m along the bank as shown. Grant swims to any point on the other bank and then runs along the side of the river to point B. If he can swim at 7 km/h and run at 11 km/h, find the distance he swims (x) to minimise the time taken to reach point B. Answer to the nearest metre.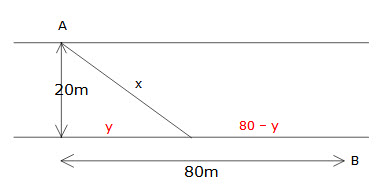
y2 = x2 – 202
$$y = \sqrt {{x^2} – 400} $$
let T = time taken where t1 is the time to swim (x) and t2 is the time to run (80 – y)
$${t_1} = \frac{x}{7}$$ and $${t_2} = \frac{{80 – y}}{{11}}$$
$$T = \frac{x}{7} + \frac{{80 – \sqrt {{x^2} – 400} }}{{11}}$$
$$T = \frac{x}{7} + \frac{{80 – {{\left( {{x^2} – 400} \right)}^{\frac{1}{2}}}}}{{11}}$$
$$T’ = \frac{1}{7} + \frac{{ – \frac{1}{2}{{\left( {{x^2} – 400} \right)}^{ – \frac{1}{2}}} \times 2x}}{{11}}$$
$$T’ = \frac{1}{7} – \frac{x}{{11\sqrt {{x^2} – 400} }}$$
$$T’ = \frac{1}{7} – \frac{x}{{11\sqrt {{x^2} – 400} }} = 0$$
$$\frac{x}{{11\sqrt {{x^2} – 400} }} = \frac{1}{7}$$
$$\frac{{{x^2}}}{{121({x^2} – 400)}} = \frac{1}{{49}}$$
49x2 = 121(x2 – 400)
49x2 = 121x2 – 48,400
–72x2 = – 48,400$${x^2} = \frac{{6050}}{9}$$
$$x = \pm \frac{{\sqrt {6050} }}{3}$$
x ≈ ±25.927
test x= 26 (to the nearest metre and x >0 as a measurement)
x 25 26 27
T’ –0.009 0 0.008
\ _ /
hence T minimum when x = 26m
