[Admin]

in reply to: Relationship between Roots and Coefficients #12008

Solve the equation 6x⁴ – 11x³ – 26x² + 22x + 24 = 0 given that the product of two of the roots is equal to the product of the other two roots.

Roots are α, β, γ, δ  and let αβ = γδ

α + β + γ + δ = ¹¹/₆

αβ + aγ + aδ + βγ + βd + γδ = –¹³/₃

αβγ + αβδ + αγδ + βγδ = ^–11/₃

αβγδ = 4

If αβ = γδ then

αβ.αβ = 4
(αβ)² = 4

αβ = ±2

αβγ + αβδ + αγδ + βγδ = ^–11/₃

αβγ + αβδ + α.αβ + β.αβ = ^–11/₃

αβ(γ + δ + α + β) = ^–11/₃

We know that: α + β + γ + δ = ¹¹/₆

αβ × ¹¹/₆ = ^–11/₃

αβ = –2    so we must discard the previous result of αβ = ±2 and just use αβ = –2 as it will satisfy both equations

If αβ = –2, then γδ = –2

αβ + αγ + αδ + βγ + βδ + γδ = –¹³/₃

–2 + αγ + αδ + βγ + βδ + –2 = –¹³/₃

αγ + αδ + βγ + βδ = –¹/₃

α(γ + δ) + β(γ+ δ) = –¹/₃

(α + β)(γ + δ) = = –¹/₃

If α + β + γ + δ = ¹¹/₆  then γ + δ = ¹¹/₆ – (α + β)

(α + β)[¹¹/₆ – (α + β)]= = –¹/₃

Let α + β = m

m(¹¹/₆ – m) = –¹/₃

¹¹/₆m – m² = –¹/₃m

11m – 6m² = –2

6m² – 11m – 2 = 0

(6m + 1)(m – 2) = 0

m = –¹/₆ or 2

when m = –¹/₆              when m = 2

α + β = –¹/₆                  α + β = 2

As αα = –2

α = –²/β

–²/_β + β = –¹/₆             –²/_β + β = 2

–2 + β² = –^β/₆              –2 + β² = 2β

–12 + 6β² = –β             β² – 2β – 2 = 0

6β² + β – 12 = 0          $$\beta  = \frac{{ – 2 \pm \sqrt {4 – 4 \times 1 \times  – 2} }}{2}$$     

(3β – 4)(2β + 3) = 0    $$\beta  = \frac{{ – 2 \pm 2\sqrt 3 }}{2}$$  

β = ⁴/₃, –³/₂, –1 ± √3

Since β is a root, then the above solutions can represent any root

Thus solution will be

x = ⁴/₃, –³/₂, –1 ± √3

[Admin]

in reply to: Relationship between Roots and Coefficients #12005

<p>Please help with Fitz Exercise 2.5 Q16 </p>

[Admin]

in reply to: Unknown Denominator Inequalities #11990

Solve $$\frac{{3x + 1}}{{x – 4}} \ge \frac{1}{3}$$.

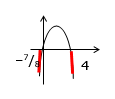3(x – 4)(3x + 1) ≥ (x – 4)²
0 ≥ (x – 4)² – 3(x – 4)(3x + 1)
0 ≥ (x – 4){(x – 4) – 3(3x + 1)}
0 ≥ (x – 4)(x – 4 – 9x – 3)
0 ≥ (x – 4)(–8x – 7)
0 ≥ –(x – 4)(8x + 7)
x ≤ –⁷/₈, x > 4

 

[Admin]

in reply to: Unknown Denominator Inequalities #11988

<p>Math In Focus EX 3.10 Q 16</p>
<p>thanks!</p>

[Admin]

in reply to: Relationship between Roots and Coefficients #11963

If the roots of the equation x³ + px² + qx + r = 0 are consecutive terms of a geometric series, prove that q³ = p³r.  Show that this condition is satisfied for the equation 8x³ – 100x² + 250x – 125 = 0 and solve this equation.

let the terms of the GP be $$\frac{a}{b},\,a,\,ab$$

$$\alpha+\beta+\gamma=\frac{a}{b}+a+ab=-p$$

$$a(\frac{1}{b}+1+b)=-p$$

$$\frac{-p}{a}=(\frac{1}{b}+1+b)$$

$$\alpha\beta+\alpha\gamma+\beta\gamma=\frac{a}{b}.a+\frac{a}{b}.ab+a.ab=q$$

$$\frac{a^2}{b}+a^2+a^2b=q$$

$$a^2(\frac{1}{b}+1+b)=q$$

$$\frac{q}{a^2}=(\frac{1}{b}+1+b)$$

$$\alpha\beta\gamma=\frac{a}{b}.a.ab=r$$

$$a^3=r$$

$$\frac{q}{a^2}=\frac{-p}{a}$$

$$\frac{-q}{p}=a^3$$ 

and $$a^3=r$$

so $$\frac{-q}{p}=r$$

$$q^3=p^3r$$

$$x^3-\frac{100}{8}x^2+\frac{250}{8}x-\frac{125}{8}=0$$

$$x^3-\frac{25}{2}x^2+\frac{125}{4}x-\frac{125}{8}=0$$

$$p=-\frac{25}{2},\,q=\frac{125}{4},\,r-\frac{125}{8}$$

$$q^3=(\frac{125}{4})^3$$

$$=\frac{1953215}{64}$$

$$p^3r=(\frac{-25}{2})^3\times\frac{-125}{8}$$

$$=\frac{1953215}{64}$$

∴ q³ = p³r is satisfied for this equation

hence

$$a^3=-\frac{-125}{8}$$

$$a=\frac{5}{2}$$

$$a(\frac{1}{b}+1+b)=-p$$

$$\frac{5}{2}(\frac{1}{b}+1+b)=\frac{100}{8}$$

$$\frac{1+b+b^2}{b}=5$$

1 + b + b² = 5b

b² – 4b + 1 = 0

$$b=\frac{4\pm\sqrt{16-4(1)(1)}}2$$

$$b=\frac{4\pm\sqrt{12}}2$$

$$b=\frac{4\pm2\sqrt{3}}2$$

b = 2 ± √3

hence roots 

$$x=\frac{5}{2},\,\frac{5}{2}(2\pm\sqrt{3})$$

[Admin]

in reply to: Relationship between Roots and Coefficients #11960

could i please get help with 
Fitzpatrick Exercise 2.5 Q10

thanks!

[Admin]

in reply to: Rationalising The Denominator #11959

Simplify $$\frac{3}{{\sqrt 5  + 2}} – \frac{{\sqrt 2 }}{{2\sqrt 2  – 1}}$$ writing your answer with a rational denominator.

$$=\frac{3}{{\sqrt 5  + 2}} \times \frac{{\sqrt 5  – 2}}{{\sqrt 5  – 2}} – \frac{{\sqrt 2 }}{{2\sqrt 2  – 1}} \times \frac{{2\sqrt 2  + 1}}{{2\sqrt 2  + 1}}$$

$$ = \frac{{3\sqrt 5  – 6}}{{5 – 4}} – \frac{{4 + \sqrt 2 }}{{8 – 1}}$$

$$ = 3\sqrt 5  – 6 – \frac{{4 + \sqrt 2 }}{7}$$

$$ = \frac{{21\sqrt 5  – 42 – 4 – \sqrt 2 }}{7}$$

$$ = \frac{{21\sqrt 5  – 46 – \sqrt 2 }}{7}$$

 

[Admin]

in reply to: Rationalising The Denominator #11958

<p>MG Test Yourself 2 Q20</p>

[Admin]

in reply to: Relationship between Roots and Coefficients #11954

If α and β are the roots of the equation x² + mn + n = 0, find the roots of nx² + (2n – m²)x + n = 0 in terms of α and β.

$$\alpha+\beta=\frac{-m}{1}$$     $$\alpha\beta=\frac{n}{1}$$

$$\alpha+\beta=-m$$     $$\alpha\beta=n$$

let p and q be the roots of nx² + (2n – m²)x + n = 0
$$p+q=\frac{-(2n-m^2)}{n}$$         $$pq=\frac{n}{n}$$

$$p+q=\frac{(m^2-2n)}{n}$$         $$pq=1$$

$$p=\frac{1}{q}$$

$$q+\frac{1}{q}=\frac{(\alpha+\beta)^2-2\alpha\beta}{\alpha\beta}$$

$$q+\frac{1}{q}=\frac{\alpha^2+2\alpha\beta+\beta^2-2\alpha\beta}{\alpha\beta}$$

$$q+\frac{1}{q}=\frac{\alpha^2+\beta^2}{\alpha\beta}$$

$$q+\frac{1}{q}=\frac{\alpha}{\beta}+\frac{\beta}{\alpha}$$

hence $$q=\frac{\alpha}{\beta}$$ and $$\frac{1}{q}=\frac{\beta}{\alpha}$$ 

and $$p=\frac{\beta}{\alpha}$$

[Admin]

in reply to: Factor Theorem #11952

Let P(x) = (x – 1)(x + 3)Q(x) + ax + b where Q(x) is a polynomial and a and b are real numbers. The polynomial P(x) has a factor of (x + 3). When P(x) is divided by (x – 1) the remainder is 8. Find the values of a and b.

P(-3) = 0   P(1) = 8

(-3 – 1)(-3 + 3)Q(3) – 3a + b = 0

-3a + b = 0

(1 – 1)(1 + 3)Q(1) + a + b = 8

a + b = 8
-3a + b = 0

a – -3a = 8

4a = 8

a = 2

2 + b = 8

b = 6

∴ a = 2, b = 6

[Admin]

in reply to: Factor Theorem #11951

<p>Fitzpatrick Exercise 2.3, Q12a </p>

[Admin]

in reply to: Remainder Theorem #11942

When 3x³ – ax² – bx + 1 is divided by (x – 2) the remainder is 5, when divided by (x – 1) there is no remainder. Find a and b.

P(2) = 5   and P(1) = 0

3(2)³ – a(2)² – 2b + 1 = 5         3(1)³ – a(1)² – b + 1 = 0

24 – 4a – 2b + 1 = 5                     (3 – a – b + 1 = 2) × 2

6 – 2a – 2b + 2 = 0

18 – 2a – 1 = 5

-2a = -12

a = 6

3 – 6 – b + 1 = 0

-b – 2 = 0

b = -2

∴ a = 6, b = -2

[Admin]

in reply to: Volume #11936

The area bounded by the curve y = x² and the line y = x + 2 rotated about the x-axis. Find the exact volume of the solid formed.

Find where they intersect

x² = x + 2
x² – x – 2 = 0

(x +1)(x – 2) = 0

x = -1, x = 2

the line will be above the curve so the integral will be the line – the parabola

find x² for each expression 

y = x + 2 ⇒ y² = (x + 2)²
y² = x² + 2x + 4

y = x² ⇒ y² = x⁴

$$V = \pi \int_{ – 1}^2 {{x^2} + 4x + 4 – {x^4}\,dx} $$

$$ = \pi \left[ {\frac{{{x^3}}}{3} + 2{x^2} + 4x – \frac{{{x^5}}}{5}} \right]_{ – 1}^2$$

$$ = \pi \left\{ {\left( {\frac{8}{3} + 8 + 8 – \frac{{32}}{5}} \right) – \left( {\frac{{ – 1}}{3} + 2 – 4 + \frac{1}{5}} \right)} \right\}$$

$$ = \frac{{72\pi }}{5}u^3$$

[Admin]

in reply to: Completing the Square #11927

Complete the square on $$y^2-\frac{5y}{2}$$.
Look at the coefficient of y : $$\frac52$$

halve it: $$\frac52\times\frac12=\frac54$$

square the result $${\left( {\frac{5}{4}} \right)^2}=\frac{25}{16}$$

$$y^2-\frac{5y}{2}+\frac{25}{16}={\left( {y – \frac{5}{4}} \right)^2}$$

 

[Admin]

in reply to: Unknown Denominator Inequalities #11510

Solve for x, $$\frac{4}{|x-1|}>2$$.

we don’t need to worry about the squaring as absolutes are always positive, so solve as a normal absolute inequality

it is easiest to rewrite by multiplying both sides by |x – 1|

4 > 2|x – 1|

2|x – 1| < 4

2(x – 1)  < 4                        2(x – 1) > -4

x – 1 < 2                                x – 1 > -2

x < 3                                      x > -1

since we have the asymptote of x = 1 in between the 1 and 3 we have to consider that in our inequality, so instead of -1 < x < 3

-1 < x < 3, x ≠ 1   or    -1 < x < 1,  1 < x < 3

[Author]

Posts