[Admin]

in reply to: Equations reducible to quadratics #12274

Solve: $$2^{2x+1}-5.2^x+2=0$$.
let m = 2^x

2^{2x + 1} = 2^2x . 2¹

= 2(2^x)²

= 2m²

2m² – 5m + 2 = 0

(2m – 1)(m – 2) = 0

m = ½, 2

2^x = ½, 2^x = 2

x = -1, x = 1

[Admin]

in reply to: Equations reducible to quadratics #12273

MIF (yr 11/preliminary); Challenge ex 10 Q9

[Admin]

in reply to: Quadratic Factors #12272

Factorise   x⁴ – x²y – 6y². 

to make this a little easier to see, consider x⁴ – x² – 6 as this is just a quadratic with x² instead of x
= (x² – 3)(x² + 2)  

now we can factor by simply placing the y back

= (x² – 3y)(x² + 2y)    

[Admin]

in reply to: Quadratic Factors #12271

MIF (year 11/preliminary) : challenge exercise 2, Q5 b

[Admin]

in reply to: Relationship between Roots and Coefficients #12270

If α, β and γ are the roots of 2x³ + 4x² – 5x + 6 = 0, find the value of $$\frac{1}{{\alpha \beta }} + \frac{1}{{\beta \gamma }} + \frac{1}{{\alpha \gamma }}$$

α + β + γ = -2   and αβγ = -3

= $$\frac{{\gamma  + \alpha  + \beta }}{{\alpha \beta \gamma }}$$

= $$\frac{-2}{-3}$$

= $$\frac{2}{3}$$

[Admin]

in reply to: Relationship between Roots and Coefficients #12269

3_pol_gir_08
Question 4, Part IV please!

[Admin]

in reply to: Quadratics #16861

A rancher has 360 m of fencing with which to enclose two adjacent rectangular corrals, one for cattle and one for sheep. A river forms one side of the corrals. Suppose the width of each corral is x metres.
a. Express the total area of the 2 corrals as a function of x
b. Find the domain of the function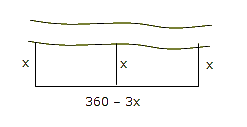

a. If x is the width out from the river, then would need 3 lots of x for fencing, leaving 360 – x for the fencing parallel to the river
A = x(360 – 3x)
A = 3x(120 – x)
b. Since this is a ‘real life’ situation, the only sensible meanings for x must be positive (since you cannot have a negative amount of fencing) so the domain will be 3x(120 – x) > 0
Domain: all real x, 0 < x < 120  or  $$D:\,\,\left( {0,120} \right)$$

[Admin]

in reply to: Function Notation #12203

Simplify $$\frac{{f(x + h) – f(x)}}{h}$$ where $$f(x)=2x^2+x$$.

first find the simplest value of ƒ(x + h) via substitution to make things a little easier

ƒ(x + h) = 2(x + h)² + (x + h)
= 2(x² + 2xh + h²) + x + h
= 2x² + 4xh + 2h² + x + h

$$\frac{{f(x + h) – f(x)}}{h} = \frac{{2{x^2} + 4xh + 2{h^2} + \,x + h – (2{x^2} + x)}}{h}$$

$$ = \frac{{4xh + 2{h^2} + h}}{h}$$

= 4x + 2h + 1

[Admin]

in reply to: Relationship between Roots and Coefficients #12072

If the sum of two roots of x⁴ + 2x³ – 8x² –18x – 9 = 0, find the roots of the equation.
roots are α, β, γ, δ
α + β + γ + δ = –2
αβ + αγ + αδ + βγ + βδ + γδ = –8
αβγ + αβδ + αγδ + βγδ = 18
αβγδ = –9

let γ + δ = 0
α + β + 0 = –2
α + β = –2

αβ + α(γ + δ) + β(γ + δ) + γδ = –8
αβ + γδ = –8

αβ(γ + δ) + γδ(α + β) = 18
αβ(0) + γδ(-2) = 18
γδ(–2) = 18
γδ = –9

αβ – 9 = –8
αβ = 1

group them into sum and products pairs
α + β = –2 and αβ = 1
forming the quadratic equation: x² – (α + β)x + αβ = 0
x² + 2x + 1 = 0

and
γ + δ = 0 and γδ = –9
x² – (γ + δ)x + γδ = 0
x² – 9 = 0

solve for x to find the roots as factors of these two quadratics will be factors of the original equation

(x + 1)² = 0    and    (x – 3)(x + 3) = 0
x = 1, 1, –3, 3

[Admin]

in reply to: Relationship between Roots and Coefficients #12063

MIF Test Yourself 12
Question 9 please!

[Admin]

in reply to: Wages & Salaries #12054

A wage sheet of a small business shows one employee’s details:
Rate per hour: $20
Normal hours: 30
Overtime (× 2): x
Wage: $840

If Nate worked some overtime at double time rate which is missing from the wage sheet, how many hours of overtime did he work?

30 hours at normal time = 30 × $20 = $600

Overtime pay =  $840 – $600
= $240

Overtime rate = double time = 2 × $20 = $40 per hour

Hours of overtime = $240  ÷ $40

= 6 hours

[Admin]

in reply to: Exact Ratios #12047

Evaluate with exact values and a rational denominator $$\frac{{1 – \cos 45}}{{1 + \cos 45}}$$.

$$ = \frac{{1 – \frac{1}{{\sqrt 2 }}}}{{1 + \frac{1}{{\sqrt 2 }}}}$$

$$ = \frac{{\frac{{\sqrt 2  – 1}}{{\sqrt 2 }}}}{{\frac{{\sqrt 2  + 1}}{{\sqrt 2 }}}}$$

$$ = \frac{{\sqrt 2  – 1}}{{\sqrt 2 }} \times \frac{{\sqrt 2 }}{{\sqrt {2 + 1} }}$$

$$ = \frac{{\sqrt 2  – 1}}{{\sqrt 2  + 1}}$$

$$ = \frac{{\sqrt 2  – 1}}{{\sqrt 2  + 1}} \times \frac{{\sqrt 2  – 1}}{{\sqrt 2  – 1}}$$

$$ = \frac{{2 – \sqrt 2  – \sqrt 2  + 1}}{{2 – 1}}$$

$$ = 3 – 2\sqrt 2 $$

[Admin]

in reply to: Equations #12033

Solve log₂ x + log₂ x³ = -8.

log₂ (x × x³) = -8

log₂ (x⁴) = -8

$${2^{{{\log }_2}{x^4}}} = {2^{ – 8}}$$

$$x^4=\frac{1}{256}$$

$$x = \frac{1}{{\sqrt[4]{{256}}}}$$

x = ¼

Note: we do not consider the negative solution x = -¼, as log x is only defined for x > 0

[Admin]

in reply to: Fractions #12028

Simplify $$\frac{{3x + 3}}{{2x}} \times \frac{{{x^2}}}{{{x^2} – 1}}$$.

$$ = \frac{{3(x + 1)}}{{2x}} \times \frac{{{x^2}}}{{(x – 1)(x + 1)}}$$

$$ = \frac{{3\cancel{(x + 1)}}}{{2\cancel{x}}} \times \frac{{{x^{\cancel{2}}}}}{{(x – 1)\cancel{(x + 1)}}}$$

$$ = \frac{3}{2} \times \frac{x}{{x – 1}}$$

$$ = \frac{{3x}}{{2(x – 1)}}$$

 

[Admin]

in reply to: Fractions #12027

11_t1_stmk_15 
St marks prelim 2015
Question 6c 

[Author]

Posts