[Admin]

in reply to: Right Angled Trigonometry #12397

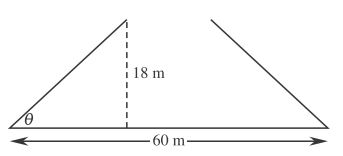A 60m long bridge has an opening in the middle and both sides open up to let boats pass underneath. The two parts of the bridge floor rise up to a height of 18m. Through what angle do they move?

Since the bridge must be without a break, then the base of each triangle will be 30m  BUT

be careful here as the 60m is the length of the road, which when it rises will be the hypotenuse of the triangles, not the base

$$\sin \theta = \frac{{18}}{{30}}$$

θ = 36°52’

[Admin]

in reply to: Trig Differentiation #12387

Find the equation of the tangent to the curve y = sin ($$\pi$$ – x) at the point ($${\textstyle{\pi \over 6}}$$, ½), in exact form.

y’ = –cos($${\textstyle{\pi \over 6}}$$ – x)
at x = $${\textstyle{\pi \over 6}}$$
y’ = –cos($$\pi$$ – $${\textstyle{\pi \over 6}}$$)
y’ = –cos  $${\textstyle{5\pi \over 6}}$$
y’ = –– $$\frac{\sqrt3}{2}$$
y’ = $$\frac{\sqrt3}{2}$$
y – ½ = (x – $${\textstyle{\pi \over 6}}$$ )
2y – 1 = √3x – √3 
12y – 6 = 6√3x –√3$$\pi$$
6√3x – 12y + 6 – √3$$\pi$$ = 0

[Admin]

in reply to: Trig Differentiation #12386

MIF (year 12) exercise 5.9 Q4

my signs are different to the answers at the back of textbook

[Admin]

in reply to: Trig Identities & Proofs #12383

Simplify $$\frac{{\tan (x + y) + \tan (x – y)}}{{1 – \tan (x + y)\tan (x – y)}}$$

let a = x + y and b = x – y

rewrite

=$$\frac{{\tan a + \tan b}}{{1 – \tan a\tan b}}$$
which is of the form

$$\tan \,(a + b) = \frac{{\tan \,a\, + \,\tan \,b}}{{1 – \tan \,a\,\tan \,b}}$$

hence
= tan (a + b)
= tan ((x + y) + (x – y)) substituting in the original values for a and b
= tan 2x

 

expanding the original is just far too difficult and leads to an impossible expression to simplify, so it is about recognising that it is the compound angle rule

[Admin]

in reply to: Integration #12333

If  $$\sec \,x\,{\mathop{\rm cosec}\nolimits} \,x = \frac{{{{\sec }^2}x}}{{\tan x}}$$, find the exact value of  $$\int_{\frac{\pi }{4}}^{\frac{\pi }{3}} {{\mathop{\rm cosec}\nolimits} \,x\,\sec \,x\,dx} $$

if y = tan x
y’ = sec²x hence
$$\int {\frac{{f'(x)}}{{f(x)}}dx = \,\ln \,x + c} $$

$$ = \int_{\frac{\pi }{4}}^{\frac{\pi }{3}} {\frac{{{{\sec }^2}x}}{{\tan x}}dx} $$

$$ = \left[ {\ln (\tan x)} \right]_{\frac{\pi }{4}}^{\frac{\pi }{3}}$$

$$ = \,\left( {\ln \,(\tan \frac{\pi }{3})} \right) – \left( {\ln (\tan \frac{\pi }{4})} \right)$$

= ln √3 – ln 1
= ln √3
= ½ ln 3

[Admin]

in reply to: Trig Differentiation #12329

Find the gradient of the tangent to the curve y = tan 3x at the point where $$x=\frac{\pi}{9}$$ .
y’ = 3sec² 3x
at $$x=\frac{\pi}{9}$$
y’ = 3 sec² 3($$\frac{\pi}{9}$$)
$$ = 3 \times \frac{1}{{{{\left( {\cos \frac{\pi }{3}} \right)}^2}}}$$
$$ = 3 \times \frac{1}{{{{\left( {{\textstyle{1 \over 2}}} \right)}^2}}}$$
= 3 × 4
= 12

[Admin]

in reply to: Trig Differentiation #12328

MIF (yr 12) ex 5.9 Q3

[Admin]

in reply to: Arc lengths, Sectors & Segments #12327

The area of a sector is $$\frac{3\pi}{10}$$ cm² and the arc length of a sector is $$\frac{\pi}{5}$$cm. Find the angle subtended at the centre of the circle and find the radius of the circle.
L = θr
$$\frac{\pi}{5}$$ = θr

$$\theta  = \frac{\pi }{{5r}}$$

A = ½r²θ

$$\frac{3\pi}{10}$$= ½r²θ

$$\frac{{3\pi }}{5} = {r^2} \times \frac{\pi }{{5r}}$$
3 = r
when r = 3

$$\theta  = \frac{\pi }{{5 \times 3}}$$

$$\theta  = \frac{\pi }{{15}}$$

[Admin]

in reply to: Arc lengths, Sectors & Segments #12326

A circle has a chord of 25mm with an angle of  $$\frac{\pi}{6}$$ subtended at the centre. Find, to 1 decimal place, the length of the arc cut off by the chord.

the chord will be bisected with a perpendicular from the centre of the circle, also bisecting the angle, which will for a right triangle with angle of $$\frac{\pi}{12}$$ at the centre and a height of 12.5cm, then using opposite over hypotenuse, sin will find the radius (hypotenuse)

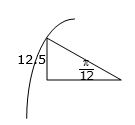$$\sin \frac{\pi }{12} = \frac{{12.5}}{r}$$

r = 48.296
L =  $$\frac{\pi }{12}$$ × 48.296
L = 25.3mm

[Admin]

in reply to: Arc lengths, Sectors & Segments #12323

MIF (yr 12) ex 5.4 Q10

[Admin]

in reply to: Arc lengths, Sectors & Segments #12322

MIF (yr 12) : Q9 EX 5.3

[Admin]

in reply to: Relationship between Roots and Coefficients #12299

Find the value of k for which 9x⁴ – 25x² + 10kx – k² is divisible by both x – 1 and x + 2. With this value of k, find the roots of the equation.

P(1) = 0
9(1)⁴ – 25(1)² + 10k(1) – k² = 0
10k – k² – 16 = 0
k² – 10k + 16 = 0
(k – 8)(k – 2) = 0
k = 8, 2
test k = 8 with P(–2) = 0
P(–2) = 9(–2)⁴ – 25(–2)² + 10(8)(–2) – 8²
= –180
≠ 0
hence k = 8 is not solution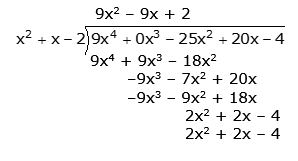
test k = 2 with P(–2) = 0
P(–2) = 9(–2)⁴ – 25(–2)² + 10(2)(–2) – 2²
= 0
hence k = 2 solution
∴ P(x) = 9x⁴ – 25x² + 20x – 4
P(x) = (x – 1)(x + 2)Q(x)
P(x) = (x – 1)(x + 2)(3x – 2)(3x – 1)

[Admin]

in reply to: Relationship between Roots and Coefficients #12297

File: 3_Pol_1

Question: 7 please

 

[Admin]

in reply to: Arranging Letters #12289

How many distinct 11- letter words can be formed from the letters of the word INDEPENDENT?

11 letters in total = 11!
repeats: 3 N’s, 2 D’s, 3 E’s

$$=\frac{{11!}}{{3!3!2!}}$$

= 554,400

[Admin]

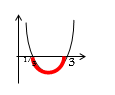
in reply to: Absolute Inequalities #12279

Solve |x + 1| > |2x – 2|.

the best way to approach an absolute inequality with absolutes on both sides is to square everyone, similar to how we deal with unknowns in the denominator – this helps us deal with the absolutes without setting up a huge amount of tests and it is far more efficient

(x + 1)² > (2x – 2)²
x² + 2x + 1 > 4x² – 8x + 4
0 > 3x² – 10x + 3
0 > (3x + 1)(x + 3)
¹/₃ < x < 3

[Author]

Posts