[Admin]

in reply to: Rates #18871

Ariane is given 1.8 litres of fluid over 10 hours by intravenous drip. The fluid is delivered at a rate of 30 drops per mL. What is the required drip rate, in drops per minute?
1.8 L × 1000 = 1800 ml	convert the 1.8 L into ml × 1000
1800 ÷ 10 = 180 ml/h	need 1800 ml over 10 hours, convert to per hour by dividing by 10
180 ÷ 30 = 3 ml/min	convert to per minute by dividing by 60 as there are 60 minutes in an hour
drops = 30 × 3 = 90 drops per minute	if each ml has 30 drops and we need 3 ml per minute, then the drops will be 30 times 3

[Admin]

in reply to: Rates #18870

Jessica received 1.8 L of fluid over 12 hours. What is the flow rate in ml/h?
1.8 × 1000 = 1800 ml	change the 1.8 L to ml  there are 1000 ml in a litre
1800 ÷ 12 = 150	so she received 1800 ml over 12 hours to find how many ml per hour, divide by the number of hours
∴ 150 ml/h

[Admin]

in reply to: Ratios #18868

The human body is made up of water, protein and bone in the ratio 7:2:1 respectively. Mary’s body contains 42kg of water. What is her total weight?
42 ÷ 7 = 6 so each part = 6 kg	Water represents 7 parts of the ratio. to find how much each part is we divide 42 by
protein = 2 × 6 = 12kg	there are 2 parts of protein, so multiply 6 by 2
bone = 1 × 6 = 6 kg	there are 1 parts of bone, so multiply 6 by 1
total mass = 42 + 12 + 6 = 60 kg	find the total weight by adding water, protein and bone

[Admin]

in reply to: Ratios #18866

Three men invest money to buy a racehorse. Joe pays $7000. Tom pays $21 000 and Dave pays $49 000. After a year, the horse has won the total prize money of $1.1 million. If the prize money is divided in the same ratio as the men invested, how much does Tom receive?
1.1 million = 1,100,000	convert the 1.1 million into a number by multiplying 1.1 by 1 000 000
Total = 7 000 + 21 000 + 49 000 = 77 000	find the total of the investments
1 100 000 ÷ 77 000 = $14.29	split the prize money into 77,000 parts to find out what each share or part is worth so each part is worth $14.29
210 00 × $14.29 = $300 090	Tom put in $21,000 so he will get 21 000 lots of $14.29

[Admin]

in reply to: Ratios #18864

Divide $1000 in the ratio 3:2.
1000 ÷ 5 = 200 ∴ each part is worth $200	there are 3 and 2 parts, which make 5 divide 1000 into 5 parts to find the value of each part
3 × 200 = $600 2 × 200 = $400 ∴ $600, $200	the first amount is 3 lots of $200 = $600 the second amount is 2 lots of $200 = $400

[Admin]

in reply to: Work Time #18862

If 5 teachers need 13 hours to mark the maths papers, how long would it take only 4 teachers?
5 × 13 = 65 hours	Step 1: Find out how long it would take for just one teacher. This will be longer, by 5 times. 1 teacher would take 5 × 13 = 65 hours
6 ÷ 4 = 1.5 days	Step 2: Find out how long it would take 4 teachers. Since there are more teachers now, it will not take as long, so we divide by how many teachers there are. 6 ÷ 4 = 1.5 days

[Admin]

in reply to: Work Time #18861

If there is enough food to last 7 people 4 days, how many days would there be enough food for 3 people?
7 × 4 = 28 days	Step 1: Find out how long the food would last for just one person. This will be longer, by 7 times. 1 person would have enough for 7 × 4 = 28 days
28 ÷ 3 = 9.3 days	Step 2: Find out how long the food would last for 3 people. Since there are more people now, it will run out more quickly, so we divide by how many people there are. 28 ÷ 3 = 9.3 days

[Admin]

in reply to: Work Time #18860

If 3 men take 2 days to dig a trench, how long would it take for 4 men?
3 × 2 = 6 days	Step 1: Find out how long it takes for one man to dig trench. This will be longer, by 3 times. 1 man will take 3 × 2 = 6 days
6 ÷ 4 = 1.5 days	Step 2: Find out how long the 4 men will take. Since there are more men now than just one, it will take shorter time, so we divide by how many men there are. 6 ÷ 4 = 1.5 days

[Admin]

in reply to: Capture-Recapture #18858

A biologist catches 100 deer in a forest, tags them and releases them back into the forest. A year later he catches 90 deer, of which 12 have tags. Estimate the total population of deer.
Total = 100 × 90 ÷ 12 = 750
	A more formal approach:
$$\frac{100}{x}=\frac {12}{90}$$	This means that 50 out of the entire population (x) was tagged, then 35 out of the 220 that were caught were tagged. As the proportion should be the same, we set them equal to each other and solve for x
$$\frac{x}{100}=\frac {90}{12}$$	First job is to ‘flip’ both fractions so the x is on the top left, making it easier to solve
$$x=\frac{90}{12} \times 100$$	Multiply by sides by 100
x = 750	round to the nearest whole number

[Admin]

in reply to: Capture-Recapture #18857

50 animals are caught and tagged and released. Later, 220 animals are caught and it is noted that 35 of these animals are tagged. What would be the total population estimate?
Total = 50 × 220 ÷ 35 = 314.28	original = 50 recaptured = 220 tagged = 35 so we can say approximately 314
	A more formal approach:
$$\frac{50}{x}=\frac {35}{220}$$	This means that 50 out of the entire population (x) was tagged, then 35 out of the 220 that were caught were tagged. As the proportion should be the same, we set them equal to each other and solve for x
$$\frac{x}{50}=\frac {220}{35}$$	First job is to ‘flip’ both fractions so the x is on the top left, making it easier to solve
$$x=\frac{220}{35} \times 50$$	Multiply by sides by 50
x = 314.28	round to the nearest whole number
x = 314

[Admin]

in reply to: Capture-Recapture #18856

The capture-recapture technique was used to estimate the population of penguins in 2013. 50 penguins were caught and tagged and then released. Later 110 penguins were captured and 20 of these were tagged. The estimated population of penguins in 2013 is 13% less than in 2012. What was the estimated population for 2012?

Total = 50 × 110 ÷ 20

= 275

hence the estimated population of 2013 is 275
since this is 13% lower than 2012 that means that 275 = 87% × x
where x is the population in 2013 and 100% reduced by 13% is 87%

x = 275 ÷ 87%
x = 316
hence the estimated population in 2012 is 316

[Admin]

in reply to: Similar Triangles #18855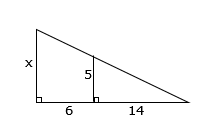

Find the value of x.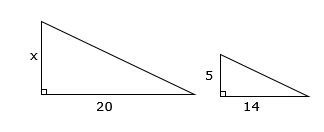
	since we have a triangle in another triangle, the first step is to separate them into the large triangle and the small triangle with the correct measurements the height of the large triangle will be x and the base will be 6 + 14 = 20 the height of the small triangle will be 5 and the base will be 14
$$\frac{x}{5}=\frac{20}{14}$$ $$^{\times\cancel{5}}\frac{x}{\cancel{5}}=\frac{20}{14}^{\times 5}$$ x = 71/7	the x matches the 5 and the 2o matches the 14 so x over 5 will equal 20 over 14 solve the equation by multiplying both sides by 5

[Admin]

in reply to: Similar Triangles #18853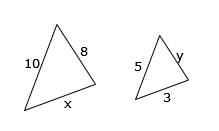

Find the value of: a. x b. y
a. $$\frac{x}{3}=\frac{10}{5}$$ $$^{\times\cancel{3}}\frac{x}{\cancel{3}}=\frac{10}{5}^{\times 3}$$ x = 6	x matches the 3, and the 10 matches the 5 be careful to make sure you are going ‘the same way’ both times. since we want x, then make it x over 3 and 10 over 5 (ie first triangle on top both times) solve the equation by multiplying both sides by 3
b. $$\frac{y}{8}=\frac{5}{10}$$ $$^{\times\cancel{8}}\frac{y}{\cancel{8}}=\frac{5}{10}^{\times 8}$$ y= 4	y matches the 8, and the 5 matches the 10 be careful to make sure you are going ‘the same way’ both times. since we want y, then make it y over 8 and 5 over 10 (ie second triangle on top both times) solve the equation by multiplying both sides by 8

[Admin]

in reply to: Similar Triangles #18851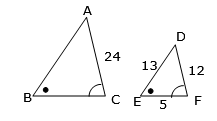

For the pair of triangles, find: a. Find the enlargement factor. b. Find the length of AB. c. Find the length BC.
a. $$\frac{12}{24}=\frac12$$	find a side in the first triangle that has a number and the matching side in the second triangle in this case it will be AC = 24 and the matching side in second triangle is DF = 12 to find the factor put the second triangle side length over the first triangle side length
b. AB = 13 × 2 AB = 26 cm	if we are looking for the side in the first triangle, the scale factor is backwards as we are going now from the second to the first triangle, so the scale factor will be the reciprocal (flip the fraction) which means the ½ will now be 2AB matches side ED = 13 multiply 13 by the scale factor of 2
c. BC = 5× 2  BC = 10 cm	BC matches side EF = 5 multiply 13 by the scale factor of 2

[Admin]

in reply to: Similar Triangles #18850

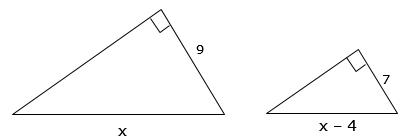Find the value of x

$$\frac{x}{x-4}=\frac{9}{x}$$ cross multiply

7x = 9(x – 4)

7x = 9x – 36

-9x -9x

-2x = -36

x = 18

[Author]

Posts