[Admin]

in reply to: BAC #18934

Calculate the BAC for Joanne if she weighs 50kg and has 4 standard drinks in 2 hours.
$$BA{C_{Female}} = \frac{{(10\times4 – 7.5\times2)}}{{5.5\times50}}$$	Use the BAC formula for a female $$BA{C_{Female}} = \frac{{(10N – 7.5H)}}{{5.5M}}$$, substituting N = 4, H = 2 and M = 50
= 0.090909	calculate
= 0.09	round correct to 2 decimal places

[Admin]

in reply to: BAC #18933

Find the value of H in the formula $$BA{C_{Male}} = \frac{{10N – 7.5H}}{{6.8M}}$$ if:

a. BAC_Male = 0.066, M = 60 and N = 5, correct to the nearest minute.

b. BAC_Male = 0.050, M = 79 and N = 7, correct to the nearest minute.

a. $$0.066=\frac{10\times5-7.5H}{6.8\times60}$$

$$0.066=\frac{50-7.5H}{408}$$  multiply both sides by 408

26.928 = 50 – 7.5H    subtract 50 from both sides

-23.072 = -7.5H   divide both sides by -7.5

H = 3.076   (change to hours and minutes)

H = 3 hours 5 minutes  

b. $$0.05=\frac{10\times7-7.5H}{6.8\times79}$$

$$0.05=\frac{70-7.5H}{537.2}$$  multiply both sides by 537.2

26.86 = 70 – 7.5H    subtract 70 from both sides

-43.14 = -7.5H   divide both sides by -7.5

H = 5.752   (change to hours and minutes)

H = 5 hours 45 minutes

[Admin]

in reply to: Medicine Dosages #18930

A child who weighs 14 kg needs to be given 15 mg of paracetamol for every 2 kg of body weight. Every 10 mL of a particular medicine contains 120 mg of paracetamol. What is the correct dosage in mL of this medicine for the child?
14 ÷ 2 = 7	find how many lots of 2 kg by dividing 14kg by 2
7 × 15 mg = 105 mg	we need 7 lots of 15 mg
105 ÷ 120 = 0.875	each 120mg is 10ml, so we need to find how many lots of 10ml we need by dividing 105 by 120
dosage = 0.875 × 10 = 8.75 ml	we need 0.875 lots of 10 ml

[Admin]

in reply to: Medicine Dosages #18928

How much of the medicine should be given to an 18 month old child if the adult dosage is 45 mL? Use Young’s Rule to make your calculations.

Dosage for children 1 to 12 years = $$\frac{{age(years) \times adult\;dosage}}{{age(years)+12}}$$

18 ÷ 12 = 1.5 years (change months to years to use in the formula)

$$ = \frac{{1.5 \times 45}}{{1.5 + 12}}$$

= 5 mL

[Admin]

in reply to: Simultaneous Equations #18926

Solve 2x – 4y = 2 and x = -2y + 9	Substitution Method this is the best method when one of the equations already say x = or y =
2(-2y + 9) – 4 = 2 -4y + 18 – 4y = 2 -8y = -16 y = 2	in this instance the second equation is x = -2y + 9 so we replace the x in the first equation with the -2y + 9 and then solve for y
x = -2(2) + 9 x = -4 + 9 x = 5	once you have solved for y, substitute into one of the first equations (try and pick the one that is the easiest) and solve for x
∴ x = 5, y = 2

[Admin]

in reply to: Simultaneous Equations #18925

Solve 2x + 3y = 4 and 2x – 4y = -10.
2x + 3y = 4 2x – 4y = -10 7y = 14 y = 2	Elimination Method this method works by adding or subtracting the equations to eliminate one of the letters and is the best method when the x‘s or y‘s are already the same since both the x’s are 2x, if we subtract them 2x – 2x = 0, so the x’s are eliminated, leaving us only with y to solve subtract: 2x – 2x = 0 3y – (-4y) = 7y    just be extra careful with the minus minus – which makes a plus solve for y
2x + 6 = 4 2x = -2 x = -1	once we have a value for y, we can substitute it back into one of the original equations (it doesn’t matter which one) to the solve for x
22x = 220	add 200 to both sides
x = 10	divide both sides by 22

 

[Admin]

in reply to: Probability #18918

A newly married couple are planning to have three children. a.   Find the sample space of all possible outcomes. b.   Find the probability of having a boy and two girls. c.   In a survey of 400 families with three children, how many of these families would you expect to have a boy and two girls?
a. BBB BBG BGB BGG GBB GBG GGB GGG	Easiest way to do this is with a tree diagram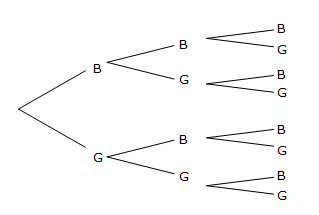
b. P(1B, 2G) = P(BGG) + P(GBG) + P(GGB) = $$\frac{1}{8}+\frac{1}{8}+\frac{1}{8}$$ = $$\frac{3}{8}$$	a boy and 2 girls is not the same as a boy then 2 girls, so we must consider all the ways this can occur
c. $$\frac{3}{8}\times400$$ = 150	to find the expected number, you multiply the probability of the result by the number in the survey

[Admin]

in reply to: Probability #18917

A dice is biased so that the chance of obtaining a 6 is twice as likely as any other number. Find: a. the probability of a 6. b. the probability of an even number c. the probability of a prime number.
a. P(6) = $$\frac27$$	List the sample space to make it easier: 1, 2, 3, 4, 5, 6, 6
a. P(Even) = $$\frac47$$	Even numbers: 2, 4, 6, 6
a. P(Prime) = $$\frac37$$	Prime numbers are: 2, 3, 5

[Admin]

in reply to: Probability #18914

Dice

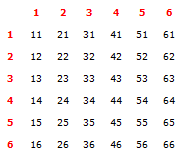
A pair of dice are rolled. What is the probability of: a. Getting doubles? b. A 6 appearing on at least one of the dice?
a. P(double) = 6/36 = 1/6	Doubles include, 11, 22, 33, 44, 55, 66 there are six of them out of a possible 36
b. P(at least one 6) = 1 – P(no 6) = 1 – P(–) = 1 – 5/6× 5/6 = 11/36	or you can count from the table, all the entries that have at least one 6: 16, 26, 36, 46, 56, 66, 61, 62, 63, 64, 65 there are 11 out of a possible 36

[Admin]

in reply to: Probability #18910

In a raffle 100 tickets are sold and there are two prizes. A woman buys 5 tickets. What is the probability that:  a. she wins neither prize  b. she wins at least one prize?
a. P(LL) = 95/100 ×  94/99   =  893/990	we need to find the probability that she loses both prizes. since she bought 5 tickets, there are 95 tickets she doesn’t have
b. 1 – P(no prizes) = 1 – 893/990 = 97/990	we just found the probability of no prizes so it will be: P(at least 1 prize) = 1 – P(no prizes)

[Admin]

in reply to: Probability #18909

Tan buys 2 tickets in a 50 ticket raffle. There are two prizes. What is the probability that Tan wins at least 1 prize?
1 – P(no, no) = 1 – 48/50 × 47/49 = 97/1225	P(at least 1 prize) = 1 – P(no prize) = 1 – P(no, no) = 1 – 48/50 × 47/49 = 97/1225 Remember: P(at least one) = 1 – P(none)

[Admin]

in reply to: Probability #18908

Steve buys three tickets in a raffle in which there is a total of 20 tickets. There are two prizes. Find the probability that he wins: a. First prize. b. First prize only. c. Both prizes. d. No prizes. e. At least one prize. f. One prize only.
a. P(W) = 3/20	He has 3 tickets, so he has 3 chances out of 20 to win first prize
b. P(WL) = 3/20 × 17/19 = 51/380	for this to occur, he has to win first prize and then lose the second prize
c. P(WW) = 3/20 × 2/19 = 3/190	to win both he must win first and then second, remembering that if he wins first prize, he only has 2 tickets left out of the 19 left to draw
d. P(LL) = 17/20 × 16/19 = 68/95	lose both prizes. if he has 3 tickets, that means there is 17 out of 20 he doesn’t have, which would then be 16 out of 19 for the second draw
e. P(at least one) = 1 – P(no prize) = 1 – 68/95 = 27/95	to find the probability of at least 1, the easiest way is to find the probability of none. So if we want at least 1 prize, find the probability of no prizes and subtract from 1
f. P(WL) + P(LW) = 3/20 × 17/19 + 17/20 × 3/19 = 51/190	only one prize could mean win first lose second, OR, lose first and win second

[Admin]

in reply to: Cards #18906

A card is drawn at random from a standard pack of 52 playing cards. Find the probability that : a. The card is not a diamond b. The card is a “number” card and is divisible by three.
a. P(not diamond) = ¾	one quarter are diamonds, so three quarters are not diamonds
b. P(number divisible by 3) = $$\frac{12}{52}$$ $$=\frac{3}{13}$$	the cards divisible by 3 are: 3, 6 and 9 there are 4 of each type = 4 × 3 = 12

[Admin]

in reply to: Cards #18905

Two cards are drawn successively at random (without replacement) from a pack of playing cards. You may assume that the pack has 52 cards of four suits. What is the probability that: a. The first card drawn is a spade? b. Both cards are spades? c. Both cards are the same suit?
a. P(spade) = ¼	there are four suits: hearts, diamonds, clubs, spades – each suit has equal chance of ¼
b. P(spade spade) = $$\frac{13}{52}\times\frac{11}{51}$$ $$=\frac{1}{17}$$	there are 13 spades so the probability of the first one is 13 out of 52, now there will only be 12 left out of 51 for the second one
c. P(same suit) = P(ss) + P(hh) + P(dd) + P(cc) $$=\frac{13}{52}\times\frac{11}{51}+\frac{13}{52}\times\frac{11}{51}+\frac{13}{52}\times\frac{11}{51}+\frac{13}{52}\times\frac{11}{51}$$ $$=\frac{4}{17}$$	we must think of all the cases where we get the same suit: 2 spades, 2 hearts, 2 diamonds, 2 clubs and add all of these probabilities

[Admin]

in reply to: Cards #18904

A card is chosen at random from a regular pack of playing cards. What is the probability that the card is: a. Red? b. A club? c. A queen? d. A black? e. The queen of hearts? f. Not a spade?
a. P(Red) = ½	half are red and half are black, so probability of red = ½
b. P(club) = ¼	there are four suits: hearts, diamonds, clubs, spades – each suit has equal chance of ¼
c. P(Queen) = $$\frac{4}{52}$$ $$=\frac{1}{13}$$	there are 4 queens out of 52 cards
d. P(Black) = ½	half are red and half are black, so probability of black = ½
e.P(Queen Hearts) = $$\frac{1}{52}$$	there is only osince ¼ are spades, then ¾ are not spades
f. P(not Spade) = ¾	since ¼ are spades, then ¾ are not spades

[Author]

Posts