[Admin]

in reply to: Projectile Motion #19104

At what angle should a particle be projected with a velocity of 50 m/s to pass through a point on its path whose coordinates are (200, 25), distances being measured in metres?

$$\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{v}$$(t) = (50cos α) + (50sin α – 10t)
$$\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{r}$$(t) = (50t cos α) +(50tsin α – 5t²)
passes through (200, 25)
x = 200, y = 25
50t cos α = 200
t = $$\frac{4}{{\cos \alpha }}$$
$$25 = 50 \times \frac{4}{{\cos \alpha }}\sin \alpha – 5 \times \frac{{16}}{{{{\cos }^2}\alpha }}$$
25 = 200tan α – 80(1 + tan² α)
25 = 200 tan α – 80 – 80tan² α
80tan² α – 200tan α + 105 = 0
16tan² α – 40tan α + 21 = 0
(4tan α – 3)(4 tan α – 7) = 0
tan α = ³/₄, tan α = ⁷/₄
a = 36°52′, 60°15′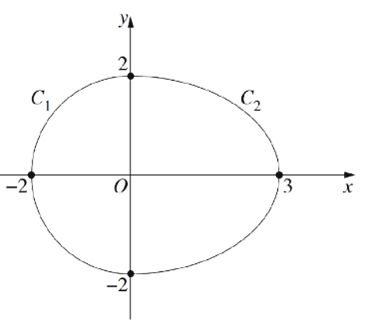

[Admin]

in reply to: Volume #19101

The diagram shows two curves C₁ and C₂. The curve C₁ is the semi-circle x² + y² = 4 for –2 ≤ x ≤ 0. The curve C₂ is the ellipse  for 0 ≤ x ≤ 3. An egg is modelled by rotating the curves about the x-axis to form a solid of revolution. Find the exact value of the volume of the solid of revolution.

[Admin]

in reply to: Integrating Inverse Trig #19097

Consider the function y = x cos^–1 x.

a. Find $$\frac{{dy}}{{dx}}$$.

$$\frac{{dy}}{{dx}} = {\cos ^{ – 1}}x\, \times \,1 + x \times – \frac{1}{{\sqrt {1 – {x^2}} }}$$

$$ = {\cos ^{ – 1}}x – \frac{x}{{\sqrt {1 – {x^2}} }}$$

b. Hence, or otherwise, evaluate $$\int\limits_0^{\frac{{\sqrt 3 }}{2}} {{{\cos }^{ – 1}}x\,dx} $$.

$$\int\limits_0^{\frac{{\sqrt 3 }}{2}} {{{\cos }^{ – 1}}x\,dx} = \int\limits_0^{\frac{{\sqrt 3 }}{2}} {{{\cos }^{ – 1}}x\,dx} – \frac{x}{{\sqrt {1 – {x^2}} }}dx + \int\limits_0^{\frac{{\sqrt 3 }}{2}} {\frac{x}{{\sqrt {1 – {x^2}} }}dx} $$

$$\left[ {x{{\cos }^{ – 1}}x} \right]_0^{\frac{{\sqrt 3 }}{2}} + \int\limits_0^{\frac{{\sqrt 3 }}{2}} {{{\cos }^{ – 1}}x\,dx} – \frac{x}{{\sqrt {1 – {x^2}} }}dx$$

$$\left[ {x{{\cos }^{ – 1}}x} \right]_0^{\frac{{\sqrt 3 }}{2}} + \int\limits_{\frac{1}{4}}^1 {\frac{{ – 1}}{{2\sqrt u }}} du$$

using substitution u = 2

$$ = \left( {\frac{{\sqrt 3 }}{2} \times \frac{\pi }{6}} \right) – \left( 0 \right) – \frac{1}{2}\int\limits_1^{\frac{1}{4}} {{u^{ – \frac{1}{2}}}} du$$

$$ = \frac{{\sqrt 3 \pi }}{{12}} + \frac{1}{2}\left[ {2\sqrt u } \right]_1^{\frac{1}{4}}$$

$$ = \frac{{\sqrt 3 \pi }}{{12}} + \frac{1}{2}$$

$$ = \frac{{\sqrt 3 \pi + 6}}{{12}}$$

 

 

 

 

[Admin]

in reply to: Differentiating Inverse Trig #19095

Suppose f(x) = tan (cos^–1 x) and g(x) = $$\frac{{\sqrt {1 – {x^2}} }}{x}$$ .
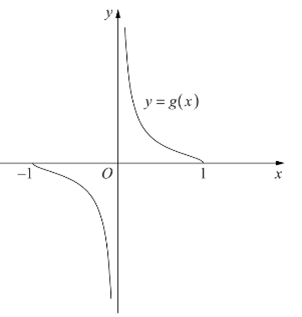
The graph of y = g(x) is shown.

a. Show that f ‘(x) = g′(x) .

f′(x) = $$ – \frac{1}{{\sqrt {1 – {x^2}} }} \times {\sec ^2}({\cos ^{ – 1}}x)$$

$$= – \frac{1}{{\sqrt {1 – {x^2}} }} \times \frac{1}{{{{\cos }^2}({{\cos }^{ – 1}}x)}}$$

$$= – \frac{1}{{\sqrt {1 – {x^2}} }} \times \frac{1}{{{x^2}}}$$

$$ = – \frac{1}{{x^2\sqrt {1 – {x^2}} }}$$

g(x) = $${(1 – {x^2})^{\frac{1}{2}}} \times {x^{ – 1}}$$

g′(x) = $$ = {x^{ – 1}} \times \frac{1}{2} \times – 2x{(1 – {x^2})^{ – \frac{1}{2}}} + \sqrt {1 – {x^2}} \times – {x^{ – 2}}$$

$$ = \frac{{ – 1}}{{\sqrt {1 – {x^2}} }} – \frac{{\sqrt {1 – {x^2}} }}{{{x^2}}}$$

$$ = \frac{{{x^2} – \sqrt {1 – {x^2}} \sqrt {1 – {x^2}} }}{{{x^2}\sqrt {1 – {x^2}} }}$$

$$ = \frac{{{x^2} – (1 – {x^2})}}{{{x^2}\sqrt {1 – {x^2}} }}$$

$$ = – \frac{1}{{x^2\sqrt {1 – {x^2}} }}$$

∴ f ′(x) = g′(x)

b. Using part a, or otherwise, show that f (x) = g(x).

if f ′(x) = g′(x) then f (x) = g(x) + c 

find c
let x = 1
f (1) = tan (cos^–1 1)
= tan 0
= 0
g(1) = 0
hence 0 = g(1) + c
0 = 0 + c
c = 0
∴  f (x) = g(x)

 

[Admin]

in reply to: Finding Terms &Coefficients #19092

In the expansion of (5x + 2)²⁰, the coefficients of x^r and x^{r + 1} are equal. What is the value of r?
(2 + 5x)²⁰
Find the term with x^r
20C_r (2)^{20 – r}(5x)^r   coefficient = ²⁰C_r (2)^{20 – r}(5)^r
Find the term with x^{r+ 1
20}C_{r + 1} (2)^{19 – r}(5x)^{r+ 1}   coefficient = ²⁰C_{r + 1} (2)^{19 – r}(5)^{r + 1}

$$\frac{{20!}}{{r!(20 – r)!}} \times {2^{20 – r}}{5^r} = \frac{{20!}}{{(r + 1)!(19 – r)!}} \times {2^{19 – r}}{5^{r + 1}}$$

divide both sides by 20! and 2^{19 – r} and 5^r

$$\frac{2}{{r(r – 1)(r – 2)…(20\, – r)(19 – r)(18 – r)…}} = \frac{5}{{(r + 1)(r)(r – 1)…(19 – r)(18 – r)…}}$$

times both sides by r(r – 1)(r – 2)… and (20 – r)(19 – r)…

$$\frac{2}{{20 – r}} = \frac{5}{{r + 1}}$$

2r + 2 = 100 – 5r
7r = 98
r = 14

 

 

 

[Admin]

in reply to: Finding Terms &Coefficients #19091

Using (1 + x)⁴(1 + x)⁹ = (1 + x)¹³, show that ⁹C₄ + ⁴C₁⁹C₃ + ⁴C₂⁹C₂ + ⁴C₃⁹C₁ = ¹³C₄.

Consider how to make x⁴ since on the RHS we are looking for ¹³C₄ 

(1 + x)⁴ = ⁴C₀ + ⁴C₁x + ⁴C₂x² + ⁴C₃x³ + ⁴C₄x⁴  and
(1 + x)⁹ = ⁹C₀ + ⁹C₁x + ⁹C₂x² + ⁹C₃x³ + ⁹C₄x⁴ + …  (don’t need to consider anything higher than x⁴ as we wont be able to multiply the two expressions to make a resulting x⁴ term with anything higher than x⁴)
term with x⁴ on both sides:
⁴C₀ × ⁹C₄x⁴ + ⁴C₁x ×  ⁹C₃x³ +  ⁴C₂x² × ⁴C₂x² +  ⁴C₃x³ ×  ⁹C₁x + ⁴C₄x⁴ ×  ⁹C₀ = ¹³C₄x⁴
let x = 1
⁹C₄ + ⁴C₁⁹C₃ + ⁴C₂⁹C₂ + ⁴C₃⁹C₁ = ¹³C₄

[Admin]

in reply to: Finding Terms &Coefficients #19090

If (1 – 2√2)⁶ = x + y√2, evaluate the value of x and y.

= $${}^6{C_0} + {}^6{C_1}( – 2\sqrt 2 ) + {}^6{C_2}{( – 2\sqrt 2 )^2} + {}^6{C_3}{( – 2\sqrt 2 )^3} + {}^6{C_4}{( – 2\sqrt 2 )^4} + {}^6{C_5}{( – 2\sqrt 2 )^5} + {}^6{C_6}{( – 2\sqrt 2 )^6}$$

= 1 – 12√2 + 120 – 320√2 +960 – 768√2 + 512
= 1593 – 1100√2
hence x = 1593 and y = –1100

 

 

[Admin]

in reply to: Finding Terms &Coefficients #19086

For the expansion of (1 + 3x)(5 – 2x)^p, find an expression for the coefficient of x².

(1 + 3x)(5 – 2x)^p = $$(1 + 3x)\left\{ {{}^P{C_0}{5^p}{{( – 2x)}^0} + {}^P{C_1}{5^{p – 1}}{{( – 2x)}^1} + {}^P{C_2}{5^{p – 2}}{{( – 2x)}^2} + {}^P{C_3}{5^{p – 3}}{{( – 2x)}^3} + {}^P{C_4}{5^{p – 4}}{{( – 2x)}^0} + {}^P{C_0}{5^{p – 5}}{{( – 2x)}^5}} \right\}$$

consider the pairings that would make x²: 1 × x² and 3x × x

$$1 \times {}^p{C_2}{5^{p – 2}}4{x^2} + 3x \times {}^p{C_1}{5^{p – 1}} – 2x$$

= $$\left( {4{}^p{C_2}{5^{p – 2}} – 6{}^p{C_1}{5^{p – 1}}} \right){x^2}$$

hence coefficient of x² is $$\left( {4{}^p{C_2}{5^{p – 2}} – 6{}^p{C_1}{5^{p – 1}}} \right)$$

[Admin]

in reply to: Rates #19074

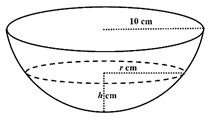
Let a hemispherical bowl of radius 10 cm contain water to a depth of h cm. The volume of water in the bowl in terms
of its depth h cm is given by V = ¹/₃πh²(30 – h) cm³.
Water is poured into the bowl at a rate of 2 cm³s^–1 .

a. If the radius of the water surface is r cm, show that $$r = \sqrt {20h – {h^2}} $$.

When the depth of water is 4 cm, find in terms of π:

b. The rate of change of the water level.

c. The rate of change of the radius of the water surface.

 

[Admin]

in reply to: Rates #19071

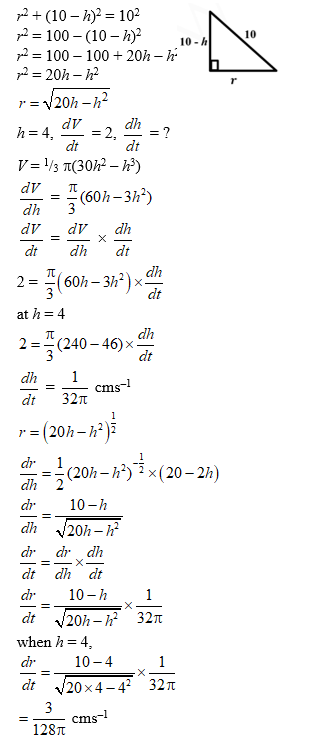
A man standing 100 metres from the base of a high–rise building observes an external lift moving up the outside wall of the building at a constant rate of 6.5 metres per second.

a. If θ radians is the angle of elevation of the lift from the observer, show that $$\frac{{d\theta }}{{dt}}$$ = $$\frac{{13{{\cos }^2}\theta }}{{200}}$$.

b. Evaluate $$\frac{{d\theta }}{{dt}}$$ at the instant when the lift is 40 metres above the observers’ horizontal line of vision.

 

[Admin]

in reply to: Rates #19069

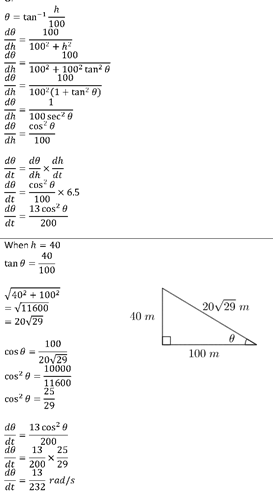
A sculptor is rolling modelling clay on a board. The clay is in the shape of a cylinder and has a constant volume of 20$$\pi$$ cm³. As she rolls it into a thinner cylinder, the radius decreases at a constant rate of 2 cm per minute. Find the rate of increase of the height h of the cylinder with respect to time, at the moment when the radius is 4 cm.

V = $$\pi$$r²h
20p = πr²h
20 = r²h
h = 20r^–2

$$\frac{{dh}}{{dr}}$$ = -40r^-3
= $$\frac{{ – 40}}{{{r^3}}}$$

$$\frac{{dr}}{{dt}}$$ = -2    $$\frac{{dh}}{{dt}}$$ = ???  when r = 4 cm 

$$\frac{{ – 40}}{{{4^3}}} = \frac{{dh}}{{dt}} \times – 2$$

$$\frac{{dh}}{{dt}} = \frac{{dh}}{{dr}} \times \frac{{dr}}{{dt}}$$

$$\frac{{dh}}{{dt}} = \frac{{ – 40}}{{{4^3}}} \times – 2$$

$$\frac{{dh}}{{dt}}$$ = 1.25 cm/s

[Admin]

in reply to: Maxima/Minima – Application Problems #19058

A window in the chapel has been damaged by a storm and needs to be replaced. It is in the shape of a rectangle surmounted by a semi-circle as shown. Let the radius of the semi-circle be r metres and the height of the rectangle be h metres.

a. Given that the perimeter of the window is to be 16π metres, show that h = 8 – r – ½πr.

$$P = h + h + 2r + \frac{1}{2} \times 2\pi r$$

16π = 2h + 2r +πr

2h = 16π – 2r – πr

h = 8π – r – ½πr

b. Hence, show that the area A of the window is given by the formula $$A = 16\pi r – 2{r^2} – \frac{1}{2}\pi {r^2}$$. 

$$A = 2r \times h + \frac{1}{2} \times \pi \times {r^2}$$

$$A = 2r \times (8\pi – r – \frac{1}{2}\pi r) + \frac{1}{2}\pi {r^2}$$

$$A =16\pi r – 2{r^2} – \pi {r^2} + \frac{1}{2}\pi {r^2}$$

$$A = 16\pi r – 2{r^2} – \frac{1}{2}\pi {r^2}$$

c. Find the exact radius of the semi-circle for which the area of the window is to be a maximum.

$$A\prime = 16\pi – 4r – \pi r$$

$$A\prime \prime = – 4 – \pi $$

0 = 16π – r(4 + π)

r(4 + π) = 16π

$$r = \frac{{16\pi }}{{4 + \pi }}$$

A′′ = –4 – π > 0 for all r

then concave down,

hence maximum when $$r = \frac{{16\pi }}{{4 + \pi }}$$

d. Find the maximum area of this window correct to 1 decimal place.

$$A = 16\pi \left( {\frac{{16\pi }}{{4 + \pi }}} \right) – 2{\left( {\frac{{16\pi }}{{4 + \pi }}} \right)^2} – \frac{1}{2}\pi {\left( {\frac{{16\pi }}{{4 + \pi }}} \right)^2}$$

A = 176.8946…

∴ maximum area = 176.9 m²

[Admin]

in reply to: ad_fn_tr.pdf #19053

Given the function g(x) = x³ – kx. Let A(–1, g(–1)) and B(1, g(1)) be two points on the graph of g.

a. Show that A is (–1, –1 + k) and B is (1, 1 – k).

b. Show that the distance AB is $$2\sqrt {{k^2} – 2k + 2} $$ , given that the distance formula is $$d = \sqrt {{{({x_1} – {x_2})}^2} + {{({y_1} – {y_2})}^2}} $$ .

a. sub the points A and B into the equation
when x = -1, y = g(-1)                  when x = 1, y = g(1)
g(-1) = (-1)³ – k(-1)                       g(1) = (1)³ – k(1)
= -1 + k                                             = 1 – k
= y                                                     = y

∴ y = k – 1                                      y = 1 – k                         
hence A(-1, -1 + k)                      B(1, 1 – k)

b. $$AB = \sqrt {{{( – 1 – 1)}^2} + {{\left( {(k – 1) – (1 – k)} \right)}^2}} $$

$$ = \sqrt {{{( – 2)}^2} + {{(2k – 2)}^2}} $$

$$ = \sqrt {4 + 4{k^2} – 8k + 4} $$

$$ = \sqrt {4{k^2} – 8k + 8} $$

$$ = \sqrt {4({k^2} – 2k + 2)} $$

$$ = 2\sqrt {{k^2} – 2k + 2} $$

 

 

[Admin]

in reply to: Projectile Motion #19045

A horizontal drainpipe 5 m above sea level empties stormwater into the sea. If the water comes out of the horizontal and reaches the sea 3 m out from the pipe, find the in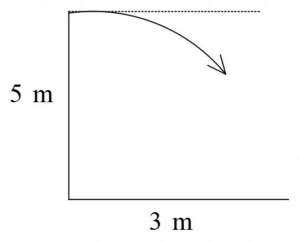initial velocity of the water. Let g = 10 ms^–2.

$$\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{a} = – 10\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{j}$$

the angle will be 0, since it is a horizontal projection

$$\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{v}(t) = (v\cos 0) \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{i}+(v\sin 0 – 10t)\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{j}$$

$$\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{v}(t) = (v) \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{i}+(– 10t)\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{j}$$

$$\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{r}(t) = (vt) \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{i}+(5–5t^2)\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{j}$$

set vertical component of displacement to 0
0 = 5 – 5t²

0 = 5(1 – t)(1 + t)

t = 1, -1

at t = 1, x = 3

3 = v

hence initial velocity is 3 ms^-1

 

[Admin]

in reply to: Substitution #18965

Under certain conditions, the power P, in watts per hour, generated by a windmill with winds blowing v kilometres per hour is given by:  P(v) = 0.015v3. How fast  must the wind blow in order to generate 120 watts of power in 1 hr?
120 = 0.015v3	substitute P(v) = 120
8000 = v3	solve the equation to find v (the speed)
v = 3√8000	take the cube root of both sides
v = 20

[Author]

Posts