Volume

[Admin]

#14990

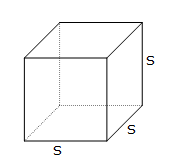
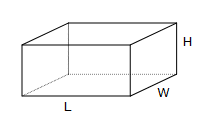
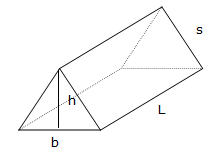
Cube $$V=s^3$$	Rectangular Prism $$V=LWH$$	Triangular Prism $$V=\frac{1}{2}bhL$$
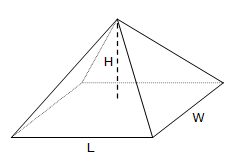
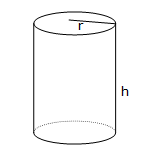
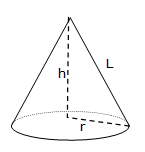
Pyramid $$V=\frac{1}{3}LWH$$	Cylinder $$V=\pi r^2h$$	Cone $$V=\frac{1}{3}\pi r^2h$$
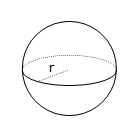
Sphere $$V=\frac{4}{3}\pi r^3$$	Truncated Cone $$V=\frac13\pi R^2\,H-\frac13\pi r^2\,h $$ or $$V=\frac13\pi(R^2\,H- r^2\,h)$$

 

 

 

 

[Admin]

#18732

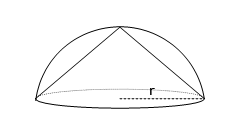The diagram shows a cone inscribed in a hemisphere. What is the ratio of the volume of the cone to the volume of the hemisphere?
a. 1:3
b. 2:3
c. 1:2
d. More information needed

Volume of hemisphere = $$\frac12\times\frac43\times\pi\times r^3$$

$$=\frac23\pi r^3$$

Volume of cone = $$\frac13\times\pi\times r^2\times h$$
since h = r

V =$$\frac13\times\pi\times r^2\times r$$

$$=\frac13\pi r^3$$

Ratio of volume of Cone to volume of Hemisphere

$$\frac13\pi r^3:\frac23\pi r^3$$

$$\frac13:\frac23$$ × both sides by 3

C 1:2

[Admin]

#18733

A cylinder has a radius of 10cm and a height of 15 cm. Find the volume.
##V=\pi\times10^2\times20## = 6283.19 cm2	V = $$\pi r^2h$$ r = 10, h = 20

[Admin]

#18734

A Christmas tree decoration in the shape of a sphere is 4.5cm in diameter. a. Find the volume of the decoration. V =4/­3πr3. b. The 12 decorations are to fit into a rectangular box which is 10cm wide and 5cm high. What is the minimum length that the box can be if it is to hold all 12 decorations?
a. V = 4/3 × π × 2.253 = 47.7cm3	Use the volume formula for a sphere: $$V=\frac{4}{3}\pi r^3$$ and calculate, where r = ½ of the diameter  radius = ½ × 4.5 = 2.25
b. 2 × 1 = 2	If it is 10cm wide, that means it can fit 2 balls across its width.
2 × 1 × 6 = 12 balls	If 5cm high, can only fit one ball.  so if we can fit two per row, and we need 12, so it has to be able to fit six rows along its length, 2 × 1 × 6 = 12 balls
6 × 4.5 = 27cm	now if each ball is 4.5cm in diameter, then 6 balls long to fit the 12, so 6 × 4.5

[Admin]

#18735

A sphere has a volume of 180m3, find the radius.
V = $$\frac43\pi r^3$$ = 180 ##r^3= 180\div\pi \div \frac43##	divide both sides by $$\frac43$$ then $$\pi$$
r3 = 42.97 r = 3.5 m	cube root both sides to find r

[Author]

Posts