Sine, Cos & Area Rules

[Admin]

#13847

Sine Rule

$$\frac{a}{\sin A}=\frac{b}{\sin B}$$

$$\frac{\sin A}{a}=\frac{\sin B}{b}$$

Cos Rule

$$a^2=b^2+c^2-2bc\cos A$$

$$\cos A=\frac{b^2+c^2-a^2}{2bc}$$

Area

$$A=\frac{1}{2}ab\sin C$$

[Admin]

#13848

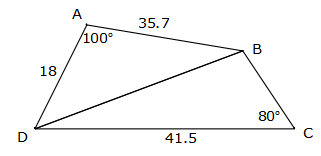Use the diagram to find: 
a. The length of BD, correct to 1 decimal place, 
b. The size of ∠DBC, correct to the nearest degree.

 

a. BD² = 18² + 35.7² – 2 × 18 × 35.7 × cos 100°
BD² = 1821.66
BD = 42.7

b. $$\frac{\sin B}{41.5}=\frac{\sin 80^{\circ}}{42.7}$$

$$\sin B=\frac{41.5\sin 80^{\circ}}{42.7}$$

B = 73°

[Admin]

#13849

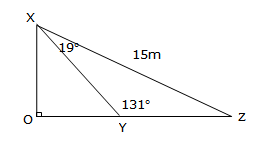Which trigonometric formula would be the most useful in calculating the length of side YZ? 

a. A = ½absin C 

b. c² = a² + b² – 2ab cos C 

c. $$\cos C=\frac{a^2+b^2-c^2}{2ab}$$

d. $$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}$$

Option A will find the area, which is not what we are after

Option B is the cos rule looking for a side, which requires two sides and the included angle, and for you to be looking for the side opposite the angle, which we do not have here

Option C is the cos rule looking for an angle, and since we are looking for a side, this is no help

Option D is the correct rule, as it is the sin rule, which requires pairs of angles/sides. the 19° is opposite YZ and the 131° is opposite the 15m

∴ D

[Admin]

#13863

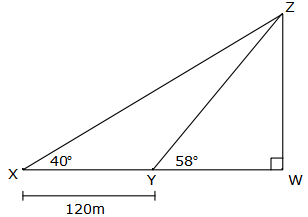Use the diagram to find: 

a. The length of XY. 

b. The length of YZ.

a. $$\frac{YZ}{\sin40^{\circ}}=\frac{120}{\sin18^{\circ}}$$ $$YZ=\frac{120\sin40^{\circ}}{\sin18^{\circ}}$$

YZ = 249.6m

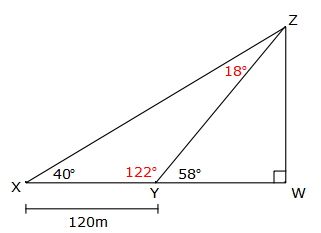b. $$\cos58^{\circ}=\frac{WY}{249.6}$$

WY =249.6 × cos 58°

WY = 132.3m

XW = XY + WY

= 120 + 132.3

= 252.3

[Admin]

#18691

In the given ΔPQR, find the angle θ to the nearest degree.

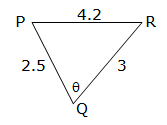
Remember that the side opposite the angle you are looking for is the side that goes into the ‘minus’ and is not on the bottom

##\cos\theta=\frac{2.5^2+3^2-4.2^2}{2\times2.5\times3}##
θ = 99°

[Admin]

#18692

ABCD is a quadrilateral in which AB = 14 cm, BC = 10 cm, AD = 17.5 cm, ∠A = 50° and ∠C = 55°.
a. Find BD.
b. Find ∠BDC.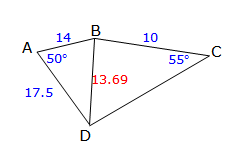

a. BD² =  14² + 17.5² – 2 × 17.5 × 14 × cos 50º
BD² = 187.2840713
BD = 13.69 cm

 

b. $$\frac{\sin D}{10} = \frac{\sin 55}{13.69}$$

$$\sin D = 10\times\frac{\sin 55}{13.69}$$

sin D = 0.598

D = 37°

[Admin]

#18693

A parallelogram, has adjacent sides of length 7cm and 5.2 cm and included angle 130°. Calculate its area correct to 1 decimal place.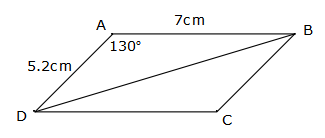
	Draw a parallelogram, including all the given information Join the diagonal opposite the obtuse angle
##A=\frac{1}{2}\times 5.2\times7\times\sin 130^{\circ}##	Using the area rule A = ½ab sin C, where a and b are the sides and C is the included angle
A = 13.942	calculate
Area = 2 × 13.942 A = = 27.884 = 27.9 cm²	We have just found the area of ΔABD, to find the area of the parallelogram, double this area round, correct to 1 decimal place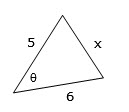

[Admin]

#18695

Find the value of sin θ if the area of this triangle is 10cm2.
10 = ½ × 6 × 5  × sin θ	Using the area rule A = ½ab sin C, where a and b are the sides and C is the included angle
10 = 15  sin θ	A = 10, and the sides a and b will be 5 and 6 substitute and simplify ½ × 6 × 5 = 15
sin θ = $$\frac{10}{15}$$	divide both sides by 15
sin θ = $$\frac{2}{3}$$	do not find the angle, be careful here, and make sure you answer the question, which is to find sin θ, not the actual size of the angle itself

[Admin]

#18697

Newcastle player Matthew Johns is attempting to kick a goal through the posts with uprights at G and P. He is 28 metres from one goal post, 32 metres from the other and the goal posts are 7 metres apart. a. Draw a diagram to show this information. b. Within what angle does he need to kick the ball to successfully convert the goal, correct to the nearest degree?
a.	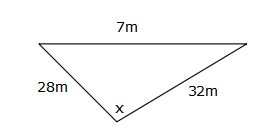we use the cos rule, as we have three sides and are looking for an angle
##\cos x=\frac{28^2+32^2-7^2}{2\times28\times32}##	noticing that the 7 is opposite the angle x, that is the one that must go into the minus at the end of the top line, the other two numbers can be put in any order
cos x = 0.98125848214	because we are looking for an angle, we must now press cos-1 to find the value of x. Press shift cos ANS on your calculator to find the angle
x = 11º

[Admin]

#18702

A tower is observed from 2 points A and B which are 240 metres apart. The angle TAB is found to be 57° and the angle TBA, 78°. Find the distance of the tower from A?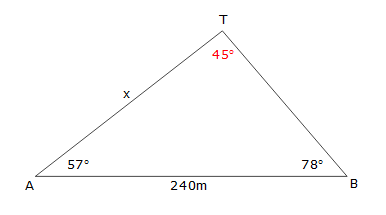
Draw a diagram to include the information given, and we can find the third angle using angle sum of Δ = 180°
$$\frac{x}{\sin78}=\frac{240}{\sin45}$$	remember with the Sin Rule, the sides and angles are ‘pairs’ and always are the ones opposite each other, so if we want the x, it is opposite 78° and the 240 is opposite the 45° always start with the thing you want on the top of the first fraction for easier calculations
$$x=\frac{240\times\sin78}{\sin45}$$	multiply both sides by sin 78
x = 331.9943	calculate
x = 332m (to the nearest metre)	since there was no indication about rounding, use your judgement, and round as you like, but make sure you round correctly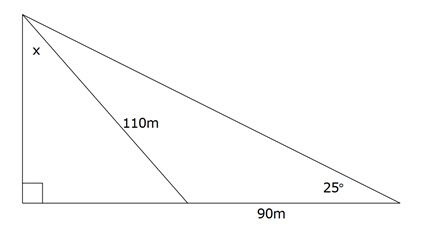

[Admin]

#18703

Find  the value of x, correct to the nearest degree.

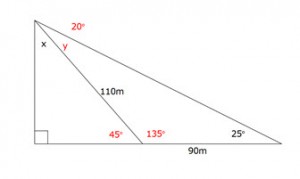Find y first, using the Sine Rule

$$\frac{\sin y}{90}=\frac{\sin25}{110}$$

$$\sin y=\frac{90\sin25}{110}$$

y = 20°

now we can find the other angle in the triangle = 180° – 25° – 20°
= 135°

now on the straight line: 180° – 135° = 45°

in the right triangle, 180° – 90° – 45° = 45°

∴ x = 45°

[Author]

Posts