Similar Triangles

[Admin]

#15100

Similar Triangles

the scale factor is what you need to times the side in the first triangle to get the number in the second triangle

scale factors can be expressed in two ways

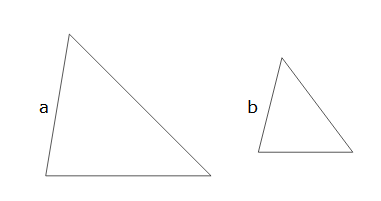
Going from first triangle to second: $$\frac{b}{a}$$\

or going from second triangle to first: $$\frac{a}{b}$$

[Admin]

#15102

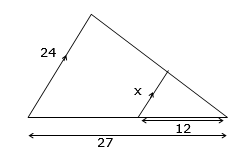Find the value of x

$$\frac{x}{24}=\frac{12}{27}$$
$$^{\cancel{24}\times}\frac{x}{\cancel{24}}=\frac{12}{24}\times 27$$

x = 10²/₃

[Admin]

#15103

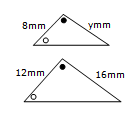
Find y in the pair of similar triangles

$$\frac{y}{16}=\frac{8}{12}$$
$$^{\cancel{16}\times}\frac{y}{\cancel{16}}=\frac{8}{12}\times16$$

y = 10²/₃

[Admin]

#15104

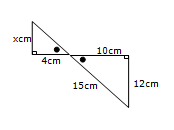Find the value of x

$$\frac{x}{12}=\frac{4}{10}$$
$$^{\cancel{12}\times}\frac{x}{\cancel{12}}=\frac{4}{10}\times12$$
x = 4.8cm

[Admin]

#18850

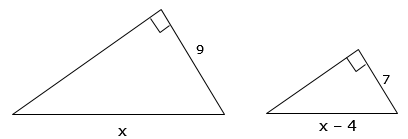Find the value of x

$$\frac{x}{x-4}=\frac{9}{x}$$ cross multiply

7x = 9(x – 4)

7x = 9x – 36

-9x -9x

-2x = -36

x = 18

[Admin]

#18851

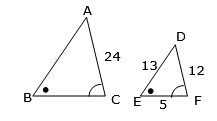For the pair of triangles, find: a. Find the enlargement factor. b. Find the length of AB. c. Find the length BC.
a. $$\frac{12}{24}=\frac12$$	find a side in the first triangle that has a number and the matching side in the second triangle in this case it will be AC = 24 and the matching side in second triangle is DF = 12 to find the factor put the second triangle side length over the first triangle side length
b. AB = 13 × 2 AB = 26 cm	if we are looking for the side in the first triangle, the scale factor is backwards as we are going now from the second to the first triangle, so the scale factor will be the reciprocal (flip the fraction) which means the ½ will now be 2AB matches side ED = 13 multiply 13 by the scale factor of 2
c. BC = 5× 2  BC = 10 cm	BC matches side EF = 5 multiply 13 by the scale factor of 2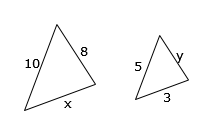

[Admin]

#18853

Find the value of: a. x b. y
a. $$\frac{x}{3}=\frac{10}{5}$$ $$^{\times\cancel{3}}\frac{x}{\cancel{3}}=\frac{10}{5}^{\times 3}$$ x = 6	x matches the 3, and the 10 matches the 5 be careful to make sure you are going ‘the same way’ both times. since we want x, then make it x over 3 and 10 over 5 (ie first triangle on top both times) solve the equation by multiplying both sides by 3
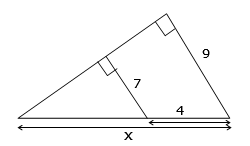
b. $$\frac{y}{8}=\frac{5}{10}$$ $$^{\times\cancel{8}}\frac{y}{\cancel{8}}=\frac{5}{10}^{\times 8}$$ y= 4	y matches the 8, and the 5 matches the 10 be careful to make sure you are going ‘the same way’ both times. since we want y, then make it y over 8 and 5 over 10 (ie second triangle on top both times) solve the equation by multiplying both sides by 8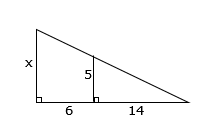

[Admin]

#18855

Find the value of x.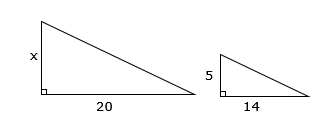
	since we have a triangle in another triangle, the first step is to separate them into the large triangle and the small triangle with the correct measurements the height of the large triangle will be x and the base will be 6 + 14 = 20 the height of the small triangle will be 5 and the base will be 14
$$\frac{x}{5}=\frac{20}{14}$$ $$^{\times\cancel{5}}\frac{x}{\cancel{5}}=\frac{20}{14}^{\times 5}$$ x = 71/7	the x matches the 5 and the 2o matches the 14 so x over 5 will equal 20 over 14 solve the equation by multiplying both sides by 5

[Author]

Posts