Probability

[Admin]

#14856

A box contains blue, red and white marbles. Write an algebraic expression for:
a. The probability of a blue marble.
b. The probability of a blue or white marble.
c. the Probability for a not blue marble.

total amount of marbles = b + r + w

a. P(B) = $$\frac{b}{b+r+w}$$

b. P(B or W) = $$\frac{b+w}{b+r+w}$$

c. P(not B) = $$\frac{r+w}{b+r+w}$$

[Admin]

#14857

In a game of football, Team A has a 41% chance of beating Team B, while team B has a 51% chance of beating Team A.
a. What is the other outcome?
b. What is the probability of this outcome?

a. Draw
b. Team A has a 41% chance of winning
P(Win) = 41%
Team B has a 51% chance of winning which means Team A has a 51% chance of losing
P(Lose) = 51%
the probability of a draw will be 100% – 41% – 51%
= 8%

∴ P(Draw) = 8%

[Admin]

#14858

Tracey is twice as likely to solve a maths problem as Terry is. If Tracey has a 25% chance of solving the problem. What are the chances of both Terry and Tracey solving the problem?

If Tracey is twice as likely as Terry, that means the Terry is half of Tracey.
Half of 25% is 12.5%
converting these to decimals P(Tracey Right) = 0.25    
P(Terry Right) = 0.125  
P(both are right) = 0.25 × 0.125
= 0.03125 =
3.125% or ¹⁄₃₂

[Admin]

#14860

For a guessing competition, a jar contains 5 red marbles and an unknown number of white marbles. Jason selected a marble at random from the jar, recorded its colour, and then replaced the marble in the jar. He repeated this procedure until he had made 200 draws. His results showed a red marble being selected 17 times. Predict the total number of marbles in the jar.

he got ¹⁷/₂₀₀ red, so that should be the same as ⁵/_x since they would be in the same proportion.

we get this equation: $$\frac{5}{x}=\frac{17}{200}$$

Flip both sides to make it easier

$$\frac{x}{5}=\frac{200}{17}$$

$$x=5\times\frac{200}{17}$$

x = 58.8

so approximately 59 marbles in

[Admin]

#18899

At a tropical holiday resort, the probability of rain on any day is 0.8. What is the probability that it will rain on a particular weekend?
P(rain on the weekend) = P(RR) + P(R-) + P(-R) = (0.8 × 0.8) + (0.8 × 0.2) + (0.2 × 0.8) = 0.96	we must consider all of the possibilities Rain on both Sat and Sun: R R Rain on Sat but not Sun: R – Rain on Sun but not Sat: – R

[Admin]

#18900

Five cards are numbered 1, 2, 3, 4 and 5. Two cards are selected and placed together to form a 2-digit number. a. What is the probability of forming the number 43? b. What is the probability of an even number occurring?
12, 13, 14, 15 21, 23, 24, 25 31, 32, 34, 35 41, 42, 43, 45 51, 52, 53, 54	work out all of the possible digits doing this in an organised table is the most efficient and easy way
a. P(43) = 1/20	there are 20 numbers altogether and only one that forms 43
a. P(even) = 8/20 = 2/5	counting the even numbers, there are 8 of them

[Admin]

#18902

There is a 9 in 10 chance of a bird hatching and surviving in the Nullarbor Plain. From a nest of 3 chicks, find the probability that: a. All 3 chicks survive. b. No chicks survive. c. Exactly 2 chicks will survive.
a. P(SSS) = 9/10 × 9/10 × 9/10 = 729/1000	P(Survive) = 9/10  P(Dead) = 1/10 for them all to survive, there is only one way this can happen SSS
b. P(DDD) = 1/10 × 1/10 × 1/10 = 1/1000	for none to survive they all must be dead: DDD
c. P(2S, 1D) = P(SSD) + P(SDS) + P(DSS) =  9/10 × 9/10 × 1/10 +  9/10 × 1/10 × 9/10 +  1/10 × 9/10 × 9/10 = 243/1000	for 2 to survive, must consider all the ways this can happen SSD  where the first 2 survive and the last one dies SDS where the middle one dies DSS where the first one dies

[Admin]

#18908

Steve buys three tickets in a raffle in which there is a total of 20 tickets. There are two prizes. Find the probability that he wins: a. First prize. b. First prize only. c. Both prizes. d. No prizes. e. At least one prize. f. One prize only.
a. P(W) = 3/20	He has 3 tickets, so he has 3 chances out of 20 to win first prize
b. P(WL) = 3/20 × 17/19 = 51/380	for this to occur, he has to win first prize and then lose the second prize
c. P(WW) = 3/20 × 2/19 = 3/190	to win both he must win first and then second, remembering that if he wins first prize, he only has 2 tickets left out of the 19 left to draw
d. P(LL) = 17/20 × 16/19 = 68/95	lose both prizes. if he has 3 tickets, that means there is 17 out of 20 he doesn’t have, which would then be 16 out of 19 for the second draw
e. P(at least one) = 1 – P(no prize) = 1 – 68/95 = 27/95	to find the probability of at least 1, the easiest way is to find the probability of none. So if we want at least 1 prize, find the probability of no prizes and subtract from 1
f. P(WL) + P(LW) = 3/20 × 17/19 + 17/20 × 3/19 = 51/190	only one prize could mean win first lose second, OR, lose first and win second

[Admin]

#18909

Tan buys 2 tickets in a 50 ticket raffle. There are two prizes. What is the probability that Tan wins at least 1 prize?
1 – P(no, no) = 1 – 48/50 × 47/49 = 97/1225	P(at least 1 prize) = 1 – P(no prize) = 1 – P(no, no) = 1 – 48/50 × 47/49 = 97/1225 Remember: P(at least one) = 1 – P(none)

[Admin]

#18910

In a raffle 100 tickets are sold and there are two prizes. A woman buys 5 tickets. What is the probability that:  a. she wins neither prize  b. she wins at least one prize?
a. P(LL) = 95/100 ×  94/99   =  893/990	we need to find the probability that she loses both prizes. since she bought 5 tickets, there are 95 tickets she doesn’t have
b. 1 – P(no prizes) = 1 – 893/990 = 97/990	we just found the probability of no prizes so it will be: P(at least 1 prize) = 1 – P(no prizes)

[Admin]

#18914

Dice

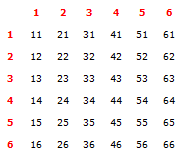
A pair of dice are rolled. What is the probability of: a. Getting doubles? b. A 6 appearing on at least one of the dice?
a. P(double) = 6/36 = 1/6	Doubles include, 11, 22, 33, 44, 55, 66 there are six of them out of a possible 36
b. P(at least one 6) = 1 – P(no 6) = 1 – P(–) = 1 – 5/6× 5/6 = 11/36	or you can count from the table, all the entries that have at least one 6: 16, 26, 36, 46, 56, 66, 61, 62, 63, 64, 65 there are 11 out of a possible 36

[Admin]

#18917

A dice is biased so that the chance of obtaining a 6 is twice as likely as any other number. Find: a. the probability of a 6. b. the probability of an even number c. the probability of a prime number.
a. P(6) = $$\frac27$$	List the sample space to make it easier: 1, 2, 3, 4, 5, 6, 6
a. P(Even) = $$\frac47$$	Even numbers: 2, 4, 6, 6
a. P(Prime) = $$\frac37$$	Prime numbers are: 2, 3, 5

[Admin]

#18918

A newly married couple are planning to have three children. a.   Find the sample space of all possible outcomes. b.   Find the probability of having a boy and two girls. c.   In a survey of 400 families with three children, how many of these families would you expect to have a boy and two girls?
a. BBB BBG BGB BGG GBB GBG GGB GGG	Easiest way to do this is with a tree diagram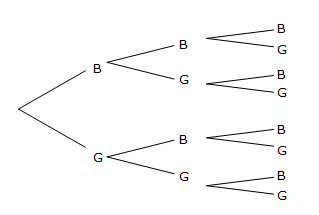
b. P(1B, 2G) = P(BGG) + P(GBG) + P(GGB) = $$\frac{1}{8}+\frac{1}{8}+\frac{1}{8}$$ = $$\frac{3}{8}$$	a boy and 2 girls is not the same as a boy then 2 girls, so we must consider all the ways this can occur
c. $$\frac{3}{8}\times400$$ = 150	to find the expected number, you multiply the probability of the result by the number in the survey

[Author]

Posts