Normal Distribution & z-scores

[Admin]

#13995

The Normal Distribution & z-scores

$$z=\frac{x-\bar{x}}{sd}$$
$$s=\frac{x-\bar{x}}{z}$$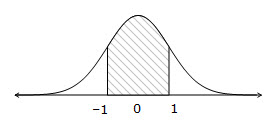

68% will lie between 1 sd above and below the mean

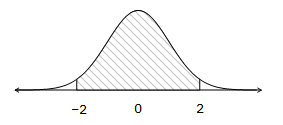
95% will lie between 2 sd above and below the mean

“very probably”

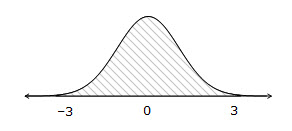
99.7% will lie between 3 sd above and below the mean

“almost certainly”

[Admin]

#14688

The scores 3, 5, 6, 7, 8, 5, 3, 5 have a mean 5.26 and standard deviation 1.64. How many of these scores are more than 1 standard deviation from the mean?
5.26 – 1.64 = 3.62
5.26 + 1.64 = 6.9
so you just count the scores under 3.62 and more than 6.9
3, 7, 8, 3
∴ 4 scores

[Admin]

#14689

The mean of set of scores is 45 and the standard deviation is 5. Between what scores do 95% of the scores lie?

95% is in between z scores of -2 and 2.
So you need 2 standard deviations below and above average.
45 – 2 × 5 = 35
45 + 2 × 5 = 55
∴ 35 – 55

[Admin]

#14693

In a normal distribution the mean is 58. A score of 70 corresponds to a standardized score of 1.5. The standard deviation of the distribution is?

$$1.5=\frac{70-58}{s}$$         substitute z = 1.5, $$\bar{x}$$= 58 and x = 70 into the formula            

1.5s = 12                                     multiply both sides by sd, and calculate 70 – 58 = 12

$$s=\frac{12}{1.5}$$           multiply both sides by sd, and calculate 70 – 58 = 12

s = 8

[Admin]

#14695

A wood saw cuts timber to an average length of 1200mm, with a standard deviation of 6mm. What are the limits of timber that would “very probably” lie between?

“very probably” means within 2 standard deviations

find the lower limit which means set 2 standard deviations below the mean 

1200 – 2 × 6 = 1188

ind the upper limit which means set 2 standard deviations above the mean 

1200 + 2 × 6 = 1212

∴ 1188mm – 1212mm

[Admin]

#14698

Michael scored 80 in his English exam where the mean was 70 and the standard deviation was 10. In Maths he scored 72 and the mean was 60 and the standard deviation was 8. Michael’s mother looked at his marks and commented: “You have performed better in English than in Maths.” Is this comment accurate? Explain.

English: $$z=\frac{80-70}{10}$$
z = 1

Maths: $$z=\frac{72-60}{8}$$
z = 1.5

Since the z-score was higher for maths, his maths score was actually better compared to the class average, so the statement is not accurate.

[Admin]

#14795

A normal distribution has mean 70 and standard deviation 5. What percentage of scores are between 65 – 70?

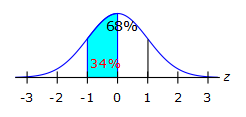$$z=\frac{65-70}{5}$$

z = -1

$$z=\frac{70-70}{5}$$

z = 0

we need the percentage of scores that lie between 0 and -1<br />
If we consider between -1 and 1, it is 68%, so from -1 to 0 would be half of that.<br />
½ × 68%<br />
∴  34%

[Admin]

#18670

In a small country town, the ages of the population are normally distributed. The mean age is 38 years and the standard deviation is 12 years. What percentage of the population lies between the ages of 38-62 is closest?

$$z=\frac{38-38}{12}$$
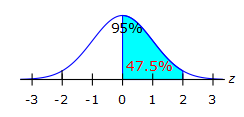= 0
$$z=\frac{62-38}{12}$$
= 2
since 95% is between -2 and 2, so 0 to 2 is half of that
47.5%

[Admin]

#18671

A set of scores is normally distributed with a mean of 50 and a standard deviation of 10. Find: a. The probability that the scores lie between 40 and 60. b. What percentage of scores will lie above 70?
a.   z = 40 – 50/10 = -1 z = 60 – 50/10 = 1	We need to find the z scores first, using the formula $$z=\frac{x-\bar{x}}{s}$$
68%	∴ the z scores are -1 and 1. This means that  of the scores will lie between 40 and 60
b. z = 70 – 50/10 = 2	Find the z-score
2.5%	since 95% lie between 2 standard deviations, that leaves 5% 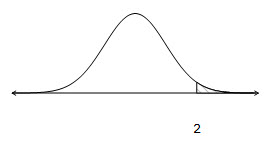for the two tails, 2.5% each. Hence the percentage over 70 will be 2.5%

[Admin]

#18672

The height of Year 12 students in the Blacktown area is distributed normally with a mean of 168 cm and a standard deviation of 7cm. a.   Between what 2 heights would 95% of the people fall? b.   What percentage of students would be between 147 cm and 189 cm tall? c.   What percentage would be taller than 175 cm? d.   If a student was selected at random, would it be very likely that they were shorter than 147 cm tall? Explain your answer.
a. 168 – 2 x 7 = 154 168 + 2 x 7 = 182 ∴ 154cm – 182cm	95% is 2 sd below and above the average find 2 standard deviations below the average find 2 standard deviations above the average
b. $$z=\frac{147 – 168}{7}$$ = -3 $$z=\frac{189-168}{7}$$ = 3 ∴  99.7% lie between 3 sd	We need to find the z scores first, using the formula $$z=\frac{x-\bar{x}}{s}$$ 99.7% of scores lie between -3 and 3 standard deviations
c. $$z=\frac{175-168}{7}$$ = 1  = 32 ÷ 2 = 16%	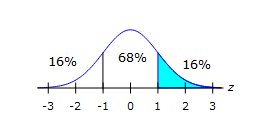Find the z score now 68% is between -1 and 1, so that leaves 32% for the two tails, now we only want more than 1 sd, so only 1 tail
d. $$z=\frac{147-168}{7}$$ =-3 so it is not likely at all as there is less than 1% chance of that happening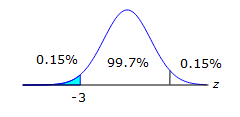	now 99.7% is between -3 and 3, so that leaves 0.3% for the two tails, now we only want less than 3 sd, so only 1 tail = 0.3 ÷ 2 = 0.15%

[Admin]

#18674

In a study of 2000 calls to insurance companies, it is found that it takes an average of 4 minutes 20 seconds for an operator to answer the phone. If the standard deviation was 40 seconds, for how many calls did the telephone operators take more than 5 minutes 40 seconds to answer the phone?
4 × 60 + 20 = 260	change the average from minutes and seconds to seconds
5 × 60 + 40 = 340	change 5 minutes 40 seconds from minutes and seconds to seconds
$$z=\frac{340-260}{40}$$ z = 2	calculate the z-score
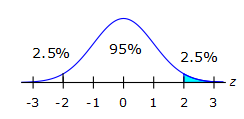
	we want to find the percentage of those above a z-score of 2 since 95% is in between -2 and 2, then that means 5% is left for above and below, split where 2.5% will be below -2 and 2.5% above 2 and we are only interested in the % higher than 2, hence 2.5%
2000 × 2.5% = 50 ∴ 50 calls took longer 2000 × 2.5% = 50 ∴ 50 calls took longer	find 2.5% of 2000

[Admin]

#18675

Steve is a marathon runner. On the Olympic course in Atlanta, the mean time is 2 hours and 15 minutes with a standard deviation of 4.5 mins. On the Sydney’s Olympic course, the mean time is 2 hours and 16 minutes with a standard deviation of 3 minutes. In Atlanta, Steve’s time was 2 hours 17 mins and in Sydney, his time was 2 hours 19 mins.? a. Write both times as standardised scores. b. Which was the better performance? Explain your answer.
a. Atlanta mean = 2 × 60 + 15 = 135 minutes Sydney mean = 2 × 60 + 16 = 136 minutes Steve’s time =  2 × 60 + 17 = 137  minutes Steve’s time =  2 × 60 + 19 = 139 minutes	convert the times to minutes for easier working
Atlanta: $$z=\frac{137-135}{4.5}$$ $$z=0.\dot4$$ Sydney: $$z=\frac{139-136}{3}$$ z = 1	work out the z score for each race
b. Sydney was the better result as the z-score was higher, which means he did better, relative to the average of the race	Any positive z score is above the average, the higher the the z-score, the better result in comparison to the mean.  A z-score of 0 is exactly the mean Any negative z score is below the average, the ‘higher’ the negative z-score, the more below average

[Author]

Posts