Linear Modelling

[Admin]

#15162

Linear Modelling

$$y = mx + c$$

where m is the gradient: $$m = \frac{{{\rm{rise}}}}{{{\rm{run}}}}$$

c is the y-intercept

[Admin]

#18823

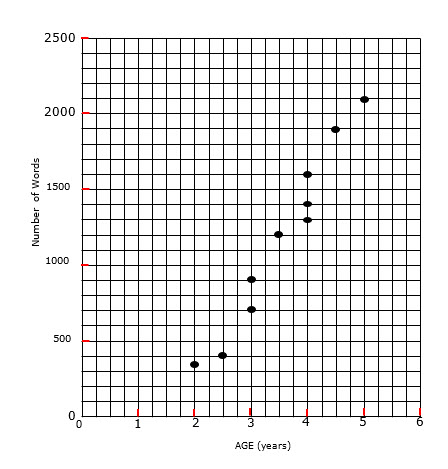
At a day care centre, the number of words that each child can use is estimated and recorded. The age of each child is also recorded. The graph shows these results.
a. Draw the line of best fit through the plotted.

b. Sally, who is three-and-a-half years old, was away from the centre on the day that this data was collected. Use your line of best fit to predict the number of words in Sally’s vocabulary.

c. From the graph, estimate at what age a child begins to use words.

d. Use your graph to estimate the average rate at which the number of words increases per year.

e. Would you expect this trend to continue as the child progresses into adulthood? Justify your answer.

 

 

 

 

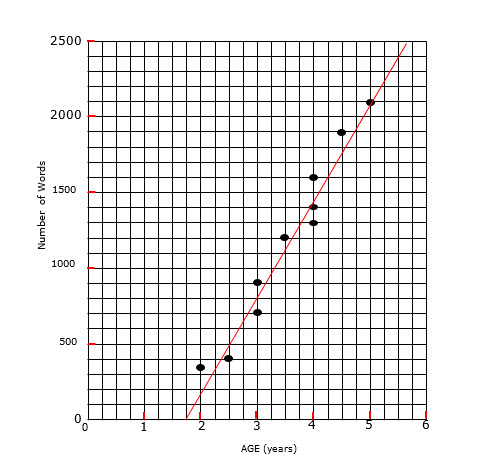a.

b. approximately 1250 (this will vary depending on your line)

c. approximately 1.8 years (find the x-intercept. this will vary depending on the line you have drawn, so they are only estimates)

d. average rate is the gradient = $$\frac{rise}{run}$$

$$=\frac{2500}{5.8-1.8}$$

= 625

(remember this will vary from graph to graph, so numbers close to this are fine)

e. no, as we learn at much faster rates when we are young, and once in high school, our vocabulary will stabilise and nowhere near as many new words will be learnt

[Admin]

#18824

The cost (C) of printing leaflets is a fixed charge $P plus an additional charge of 5 cents per copy. a. Write down a formula for the cost, in dollars, of printing 1000 leaflets. b. If the fixed charge is $300 and I paid a total of $600, how many copies did I have printed?
a.  C = P + 0.05n	change the 5c to dollars: 0.05 and that will be per leaflet, so if we let the number of leaflets be n, then the cost will be the additional cost P plus 0.05n
b. 600 = 300 + 0.05n 300 = 0.05n n = 300 ÷ 0.05 n = 6000	substitute 600 into C, 300 into P and solve for n minus 300 from both sides divide both sides by 0.05

[Admin]

#18825

V 20 40 60 80 100 T 11 21 31 41 51 From the table, write down a formula connecting V and T.
$$m=\frac{21-11}{40-20}$$	we need to get the equation in the form y = mx + c, where m is the gradient, and using the appropriate letters, which in this case will be V = mT + c
$$m=\frac{10}{20}$$ m = ½	Step 1: find the gradient The easiest way to do this is find the rise over run by taking any pair of numbers and putting the difference of the T‘s over the difference of the V‘s In this example the pairs chosen will be 20, 11 and 40, 21
T = ½T + c 11 = ½ × 20 + c 11 = 10 + c c= 1	substitute the value for m into the equation and then pick a pair (it doesn’t matter which ones) and substitute to solve for c substitute V = 2- and T = 11 solve for c
T = ½V + 1	substitute values you just found for both m and c into the equation

[Author]

Posts