Field Survey & Notebook Entries

[Admin]

#15091

Notebook Entries & Field Surveys

Area Triangle

$$A\frac{1}{2}bh$$

Pythagoras

$$c^c=a^2+b^2$$

Area Trapezium

$$A\frac{h}{2}(a+b)$$

 

 

[Admin]

#18745

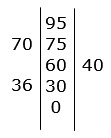a. Draw a field diagram of the block of land represented by the notebook entry.
b. Calculate the area of this block of land.

a.	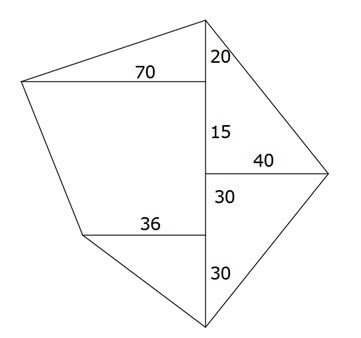draw the offsets on the left and right, including each measurement going up, starting at 30, then (60 – 30) = 30 (75 – 60) = 15 (95 – 75) = 20
b. A1 = ½ × 95 × 40 = 1900	find the area of the triangle on the right: base = 95 and height = 40
A2 = ½ × 70 × 20 = 700	Area of the top triangle on the top left: base = 70 and height = 20
A3 = ½ × 45 × (70 + 36) = 2385	Area of trapezium with height 45 and parallel sides 70 and 36
A4 = ½ × 30 × 36 = 540	Area of bottom triangle on the left: base = 30 and height 36
A = 1900 + 700 + 2385 + 540 = 5525m2	add to find the total area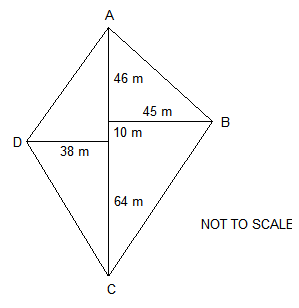

[Admin]

#18746

A field is to be converted into an olive grove. A surveyor’s sketch diagram of the field is shown. a. Calculate the area of the field. b. Each olive tree needs an area of 15 m2 to obtain maximum growth potential. What is the maximum number of trees that can be planted in the field? c. If a scale diagram of the field is drawn using a scale of 1:1000, what would be the length of AC on the scale diagram?
a. A1 = ½ × 120 × 38 = 2280 A2 = ½ × 120 × 45 = 2700 ∴ total area = 4980m2	ΔADC has base of of (64 + 10 + 46) and height of 38 ΔABC has base of of (64 + 10 + 46) and height of 45
b. 4980 ÷ 15 = 332 ∴ 332 trees	need to find out how many lots of 15 can fit into 4980, so divide by 15
c. 120m ÷ 1000 = 0.102m 0.102 × 100 = 12cm	converting from real life measurements to scale drawing, divide by the scale factor of 1000 convert the m into cm by multiplying by 100 as 100cm = 1m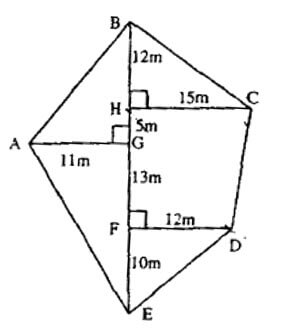

[Admin]

#18747

A traverse survey of a field is shown. a. Calculate the length of CD, correct to 2 decimal places. b. Calculate the area of the portion of the field with corners at HCDF. c. If this field was to be drawn using a scale of 1:250, calculate the length of the interval which would represent BE.
a. CD2 = 32 + 182 CD2 = 333 CD = √333 CD = 18.25m	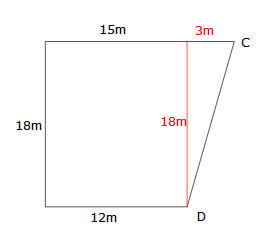Use Pythagoras to find the length of CD, the base of the triangle will be 15m – 12m = 3m and the height of the triangle will be 5m + 13m = 18m
b. $$A=\frac{18}{2}\times(15 + 12)$$ = 243m2	HCDF is the trapezium with parallel sides 15m and 12m and height 18m Area of trapezium: $$A=\frac{h}{2}(a+b)$$
c. BE = 12 + 5 + 13 + 10 = 40 m	find the total length of BE
40 ÷ 250 = 0.16m	convert to the scale factor: since we are going from real life to diagram, divide 40m by 250
=0.16m × 100 = 16 cm	convert from m to cm, by multiplying by 100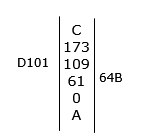

[Admin]

#18749

An offset survey of a park was conducted, and the notebook entries are shown. All measurements are in metres. a. Draw a neat sketch of the diagram. b. Calculate the distance CD, correct to the nearest metre.
a.	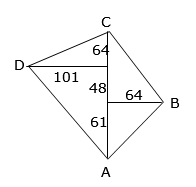line AC goes down the middle draw offset B – length 64 – on the right and offset D – length 101 -(a little above) on the left and add labels from A to the B offset is 61 from the B to the D is 109 – 61 = 48 from the D to the C at the top is 173 – 109 = 64
b. CD2 = 1012 + 642 CD2 = 14,297 CD = √14,297 CD = 119.57 ∴ CD = 120m	use Pythagoras to find the length of CD don’t forget to round correctly to the nearest metre

[Author]

Posts