Bearings – Right Trig

[Admin]

#13817

Bearings Right Trig

SOH CAH TOA

$$\sin\theta=\frac{opp}{hyp}$$

$$\cos\theta=\frac{adj}{hyp}$$

$$\tan\theta=\frac{opp}{adj}$$

[Admin]

#13818

A yacht sails due west for 45 nautical miles, before turning north for 23 nautical miles.
a. Calculate the bearing of the yacht from its starting point
b. On what bearing must the yacht sail to return to its starting point.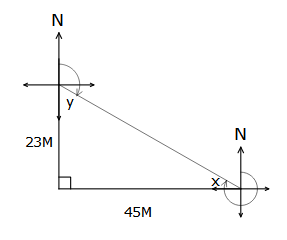

a. $$\tan x=\frac{23}{45}$$
x = 27°
∴ bearing= 270° + 27°     (remembering that it is 270° around from north to west)
= 297°

b.  y = 180° – 90° – 27°  (angle sum of Δ = 180°)
y = 63°

∴ bearing= 180° – 63°
= 117°

[Admin]

#13819

A  man starts from X and walks 2km N35°W to Y, and then turns to his right, through 90°, and walks 1km to Z.  What is the direction of Z from X?

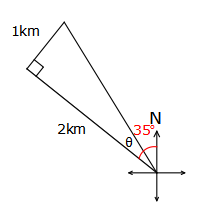$$\tan\theta=\frac{1}{2}$$

θ = 27°

the direction from North will be 35° – θ
= 35° – 27°
= 8°

∴ the direction will be N8°W

[Admin]

#13828

 A man travels 20km in the direction 330°. How far has he travelled?

This is a trick question and needs to be read carefully. A man travels 20km in the direction 330. How far has he travelled? 20km There is nothing to actually work out, it says how far he has travelled, and it asks how far he has travelled.

[Admin]

#18706

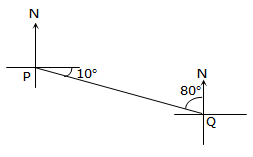The true bearing of P from Q is:

a.   080°   b.   100°   c.   280°   d.   W80°N 

 

 

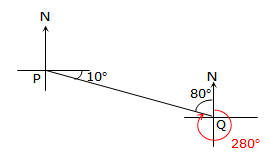
Since the bearing is P FROM Q, then we must look at the point Q
Subtract 80° from 360° to get 280°, remembering that true bearings work clockwise from north
hence C is the correct answer

[Admin]

#18707

The bearing of town A from O is N65°W and the bearing of town B 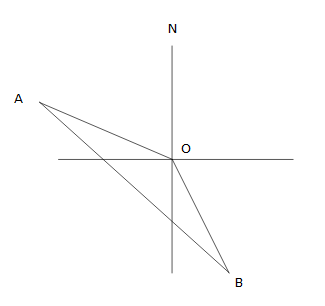from O is S50E° What is the size of ∠AOB?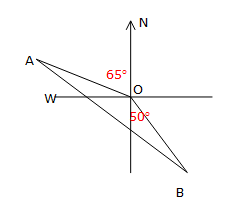
	mark on the information from the question. ∠NOA = 65° ∠SOB = 50° ∠AOW = 90° – 65°   (right angle) = 25°
∠AOB = 25 + 90 + 50 = 165°

[Admin]

#18709

A plane flies from Brisbane on a bearing of 220° at a speed of 250 km per hour. For how long (in hours and minutes must the plane fly for it be 750 km south of Brisbane?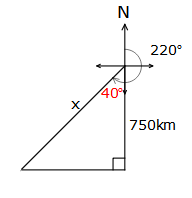
	Draw a diagram with the information on. A bearing of 220 puts it in between 180° (south) and 270° (west) Construct the triangle and the angle inside the triangle will be 40°, which is 220° – 180° We are looking for the distance the plane has flown, that is the bearing line which is the hypotenuse and we want it to be 750km south, which will be the adjacent, so use the cos ratio
##\cos40^{\circ}=\frac{750}{x}##	as the x is on the bottom, we divide, remembering to put the number first
x = 750 ÷ cos 40°	calculate
x = 979.055 km	so the distance travelled is 979.055km
$$t=\frac{979.055}{250}$$	to calculate the time, we need to use $$t=\frac{d}{s}$$
t = 3.916 hours	calculate
t = 3 h 55 minutes	to convert into hours and minutes, use the degrees and minutes button

[Author]

Posts