-
Bearings Non-Right Trig
Sine Rule
$$\frac{a}{\sin\; A}=\frac{b}{\sin\; B}$$
$$\frac{\sin\; A}{a}=\frac{\sin\; B}{b}$$Cos Rule
$$a^2=b^2+c^2-2bccos A$$
$$cos\;A=\frac{b^2+c^2-a^2}{2bc}$$Area Rule
$$A=\frac{1}{2}ab\sin\;C$$
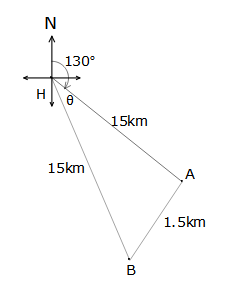Sue leaves home and walks 15km on a bearing of 130°, arriving at point A. Jessica, her sister leaves home a little after Sue and also walks 15km but due to a compass error, arrives too far south and not far enough east, arriving a part B which is 1.5 km from point A. Which bearing did Jessica take?$$\cos\theta=\frac{15^2+15^2-1.5^2}{2\times15\times15}$$
θ = 5.7º
∴ bearing = 130º + 5.7º
= 135.7°
A plane flies from Mascot Airport on a bearing of 050° at 500 knots. Another plane leaves Mascot Airport at the same time and flies on a bearing of 120° at 400 knots. (1 knot = 1 nautical mile per hour)
a. Copy and complete the information on a diagram.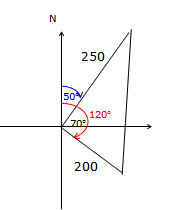
b. How far apart will the planes be after 30 minutes, correct to the nearest nautical mile?a.
b. 30 minutes is half an hour, so the first distance ½ × 500 = 250 nautical miles
the second distance ½ × 400 = 200 nautical miles
the first bearing is 50° and the second bearing is 120°, leaving the angle in between them as 120° – 50° = 70°
since we have two sides and the included angle, will be using the cos rule
x2 = 2502 + 2002 – 2 × 250 × 200 × cos 70°
x2 = 68,297.99
x = 261 nautical miles
A ship sails 40 nautical miles from A to B on a course bearing of 060°, and then 25 nautical miles due east from B to C.
a. What is the distance from A to C?
b. What is the bearing of C from A?
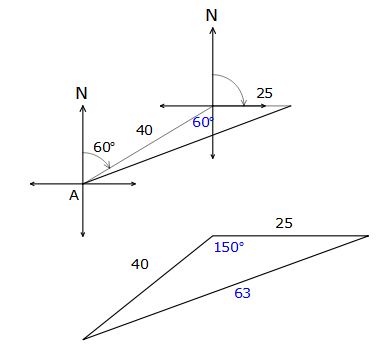
make a diagram, and label carefully
the ∠B consists of two parts, the 60°, which is an alternate ∠ in the parallel lines, and 90°, since C is due east of B 60° + 90° = 150°
a. AC2 = 402 + 252 – 2 × 40 × 25 × cos 150°
AC2 = 3957.05
AC = 63 nm
Use the cos rule to find the length of AC
b.$$\frac{\sin A}{25}=\frac{\sin 150}{63}$$
$$\sin A = 25\times\frac{\sin 150}{63}$$
use the sine rule to find ∠BAC
A = 11°
∴ 071°
now the bearing will be 60° + 11° (and don’t forget a true bearing has to have 3 digits)
A mining surveyor is travelling due east in nearly flat. To avoid a flooded area, a detour is made by first driving from A to B, a distance of 15 km, on a bearing of 062°. From B she drives southeast until rejoining the original line of travel at C.
a. Copy the diagram. Find the sizes of ∠BAC and ∠ABC, marking them on the diagram.
b. Use the Sine Rule to calculate the distance AC, give your answer to the nearest tenth of a kilometre.a. ∠BAC = 90° – 62°, as it forms a right angle, since C is due east
∠BAC = 28°
since the 62 is alternate ∠ in the parallel lines, 180 – 45° = 135°, since on a straight line and south-east means a bearing of 135°∠ABC = 62° + 45°
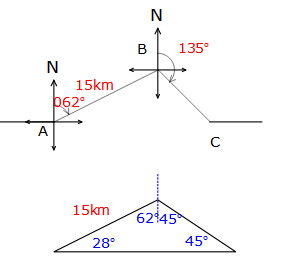
b. $$\frac{AC}{\sin 107^{\circ}}=\frac{15}{\sin 45^{\circ}}$$
$$AC=\frac{15\sin107^{\circ}}{\sin45^{\circ}}$$
AC = 20.3 km
Use the sine rule in the triangle with the angles found above to find the length of AC
- You must be logged in to reply to this topic.
