| sad number |
unhappy number, a number that is not happy |
| sample |
term in statistics when a portion of the population is tested, and that proportion is said to be representative of the whole population |
| sample space |
a list of all the possible outcomes in probability |
| satisfy |
a solution is said to satisfy an equation if it produces a true statement. For example, x = 3 satisfies the equation x + 1 = 4 |
| scalar |
a unit which has size but no direction |
| scale |
the marks on a graph or measuring instrument. For example, most rulers have a scale of 1 cm or 1 mm, sometimes both |
| scale |
a scale on a map tells us what ratio is used to compare distances on a map to distances in the real world. For example, a scale of 1:100 tells us for every 1 cm on the map, there is 100 cm, or 1 m in real life |
| scalene triangle |
triangle with no equal sides and no equal angles |
| scatter diagram |
a diagram in statistics to compare two variables by placing dots to see if a relationship between those variables can be established
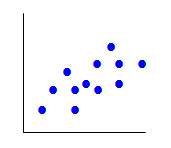 |
| scientific notation |
also known as standard notation. A system to write any number, no matter how large or small so that they are easy to write and compare. Scientific notation is of the form a x 10n where n is a positive integer if the number is more than one and n is a negative integer if the number is less then one. 4583 in scientific notation would be: 4.583 × 103 = 0.000 732 in scientific notation would be: 7.32 × 10-4 The decimal must always go after the first number and the n is the number of places you moved that decimal to put it after the first digit. |
| score |
20 |
| SD |
see standard deviation |
| sec |
the inverse of cos θ, sec θ = $$\frac$$ |
| secant |
a line which passes through at least two points of a curve or a circle |
| sector |
the part of a circle between two radii and the circumference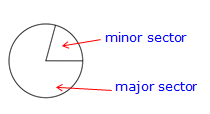 |
| segment |
the part of a circle cut off by a chord
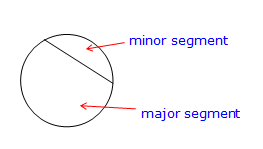 |
| selling price |
price a service or article is sold for |
| semi-circle |
half a circle |
| septagon |
polygon with 7 sides (see also heptagon) |
| sequence |
a set of numbers in a particular order or follow a particular pattern |
| series |
the name given to the sum of numbers in a sequence (or pattern) |
| set |
a group of clearly defined and identifiable members |
| sexagesimal |
number system based on 60. Used for time and angles. On your calculator it is the ° ' " button which stands for degrees, minutes and seconds |
| sigma |
Greek letter, capital sigma: Σ denoting the sum of and little sigma: σ denoting the standard deviation usually, although it can also be used to denote an unknown angle |
| sign |
the sign of a term tells us if it is positive or negative |
| significant figures |
the number of figures that are important to a number. For example, 135 836 correct to 2 significant figures would be 130 000 |
| similar |
two shapes are similar if they are exactly the same shape, just not the same size |
| similarity tests for triangles |
if all angles of one triangle are the same as the second triangle (AAA) or equiangular. If the sides about an equal angle are in equal ratio. If all side of one triangle are in equal ratio to the sides of the other triangle |
| simple harmonic motion |
SHM, the motion of a body which oscillates. The formulas associated with SHM are x = acos(nt + α) or a = –n2x |
| simple interest |
when money is invested and interest is only earned on the original amount invested. $$I=\frac$$ where I is interest, P is principle invested, R is interest rate and N is the number of periods invested for |
| simplify |
to answer a question in its most simple or basic form |
| Simpson's Rule |
used to find approximate areas of irregular shapes A = h/3(dF + 4dM + dL) or
A =h/3
|
| simultaneous |
occurring at the same time |
| simultaneous equations |
two or more equations, solving them will give you the point of intersection between them |
| sin |
sin θ = $$\frac$$ |
| sketch |
to draw without actually plotting |
| skew distribution |
a distribution not symmetrical. The first diagram is an example of a positive skew. The 'tail' is being pulled in the positive direction (ie to the right). in the second diagram, the 'tail' is being pulled in a negative direction (ie left), so is negatively skewed
 |
| skew lines |
lines that are not parallel, but do not intersect |
| slant height |
the height from the vertex to the base edge of a pyramid or cone, not the perpendicular height. In this figure the slant height is represented by the letter l or s.
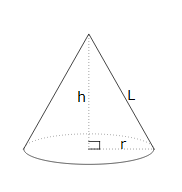 |
| small circle |
circles drawn around the earth that do not pass through the centre. All circles of latitude, except the equator are small circles
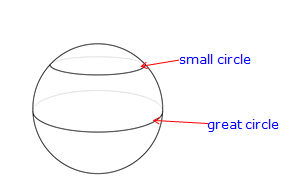 |
| solid |
three dimensional shape |
| solid of revolution |
shape formed when part of a line or curve is rotated about the x or y axis. $$V=\pi\int_^y^2\,dx$$ if rotated about x-axis. $$V=\pi\int_^x^2\,dy$$ if rotated about y-axis |
| solution |
another name for the answer to a problem |
| solve |
instruction to work out answer to question posed |
| speed |
$$speed=\frac$$
how much distance is covered in a certain time period. For example, 60 km/h means for every hour travelled, 60 km of distance will be covered |
| sphere |
round solid shape, a ball $$V=\frac43\pi r^3$$ $$SA=4\pi r^2$$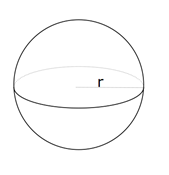 |
| spherical |
shaped like a sphere |
| spread |
statistical term to measure how far from the average the data is. Measures of spread include the range, the interquartile range, the standard deviation |
| square |
four sided shape with all sides equal, opposite sides parallel, adjacent sides perpendicular. Diagonals are equal and bisect at right angles |
| square numbers |
1, 4, 9, 16, 25, 36, 49, 64, 81, 100…. |
| square pyramid |
Solid shape with a square base and four triangular faces
. 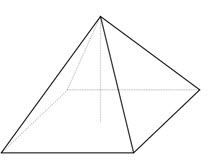 |
| square root |
to find the square root of a number we need to find a number that multiplies by itself to give us the number we want the square root of. For example 2 × 2 = 4, so the √4 = 2. 8 × 8 = 64, so the √64 = 8. |
| standard deviation |
SD measures the spread of a distribution. Essentially, the larger the standard deviation, the more spread out, the smaller the standard deviation, the less spread out, or the more consistent the scores are |
| stationary point |
the point on any curve where the tangent is parallel to the x-axis, having a gradient of zero. It is neither increasing, nor decreasing. Each stationary point must be either a maximum, minimum or a horizontal point of inflection. The stationary point can be found using $$\frac=0$$ (see also turning point) |
| straight |
line that is not curved or bent |
| straight angle |
angle of 180°
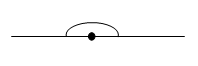 |
| subject |
the subject of an equation is the single letter that equals all the other terms. For example in y = 2x + 3z, y is the subject |
| substitution |
replacing a letter in a formula with a number, another letter or another expression |
| subtend |
is opposite to |
| sum |
to add up, find the total of |
| supplementary angles |
add to 180° |
| surd |
a number with a root that cannot be simplified into a rational number. √12 may be simplified to 2√3, but no further. All surds are irrational numbers |
| survey |
term in statistics when a portion of the population is tested, and that proportion is said to be representative of the whole population |
| symbol |
sign or letter used to represent something else. The symbol = represents 'equals'. The Greek symbol θ, theta, is used to represent unknown angles. |
| symmetric |
having symmetry |
| symmetry |
if you cut a shape in half, it will be the same on both sides |