By failing to prepare, you are preparing to fail.
Sectors & Arc Lengths2020-12-31T20:02:09+10:00

Timetable › Forums › Standard › Measurement › Sectors & Arc Lengths

Tagged: , , ,

Viewing 7 posts - 1 through 7 (of 7 total)
  • Author
    Posts
  • Admin
    Keymaster
    December 2, 2018 at 3:43 pm
    Post count: 1622
    #15034
    Area Sector
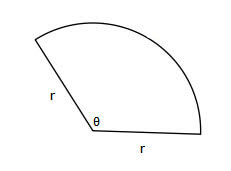
    j_mea_sector

    $$A=\frac{\theta}{360}\,\pi r^2$$

    Arc Length

    $$L=\frac{\theta}{360}\times 2\pi r$$

    Admin
    Keymaster
    December 31, 2020 at 7:45 pm
    Post count: 1622
    #18750

    What is the centre angle of a sector with an area of 15cm2 and a radius of 2.5cm? Answer correct to the nearest degree.

    $$A=\frac{\theta}{360}\times\pi\times r^2$$

    $$15=\frac{\theta}{360}\times\pi\times 2.5^2$$

    $$15\div\pi\div 2.5^2=\frac{\theta}{360}$$

    $$15\div\pi\div 2.5^2\times360=\theta$$

    θ = 275º

    Admin
    Keymaster
    December 31, 2020 at 7:45 pm
    Post count: 1622
    #18752
    Find the area of a sector with angle of 50° and a radius of 10cm, correct to 2 decimal places.
    $$A=\frac{50}{360}\times\pi \times 10^2$$ Using the formula $$A=\frac{\theta}{360}\,\pi r^2$$ where θ = 50 and r = 10
    A = 43.6332313 calculate
    A = 43.63cm2 round to 2 decimal places (don’t forget the cm2)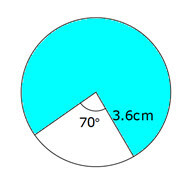
    Admin
    Keymaster
    December 31, 2020 at 7:46 pm
    Post count: 1622
    #18753
    gen_mea_sector_0001Calculate the area of shaded sector, correct to 1 decimal place.
    $$A=\frac{290}{360}\times\pi \times 3.6^2$$ have to be very careful here as the 70° is NOT in the area we are looking for. We need to find the angle in the shaded area θ = 360° – 70° = 290°
    θ =290, r = 3.6
    A = 32.79882273 calculate
    A = 32.8cm2 round to 1 decimal place
    Admin
    Keymaster
    December 31, 2020 at 8:05 pm
    Post count: 1622
    #18760

    PQ is the arc of a circle with radius r, making an angle of 50° at the centre of the circle O. Find an expression for the length of PQ?

    Arc Length = $$\frac{\theta}{360}\times2\times\pi\times r$$

    $$=\frac{50}{360}\times2\times\pi\times r$$

    $$=\frac{5\pi}{18}\times r$$

    $$=\frac{5\pi r}{18}$$

    Admin
    Keymaster
    December 31, 2020 at 8:05 pm
    Post count: 1622
    #18761
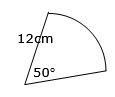    j_arc_001Find the length of the arc in this sector.
    $$L=\frac{50}{360}\times2\times\pi\times 12$$ r = 12 cm and the angle at the centre = 50°, hence θ = 50
    substitute into the formula $$L=\frac{\theta}{360}\times2\pi r$$
    L = 10.47 cm calculate
    Admin
    Keymaster
    December 31, 2020 at 8:06 pm
    Post count: 1622
    #18763
    A circle has a radius of 14 metres.
    a. Find the circumference, to the nearest 0.01m, of the circle.
    b. What is the spherical distance on this circle subtending an angle of 40° at the centre, correct to the nearest 0.01m?
    c. What is the angular distance subtended by an arc of length 10m on this circle, correct to the nearest degree?
    a. C = 2 × π × 14
    = 87.96 m    		 using the formula C = 2πr to find the circumference
    and round to 2 decimal places

    b. $$L =\frac{40}{360}\times 2\pi \times 14$$

    = 9.77 m

    		  use the arc length formula: $$L =\frac{\theta}{360}\times 2\pi r$$

    c. $$10 =\frac{\theta}{360}\times 2\pi \times 14$$

    $$\frac{\theta}{360}=10\div2\div\pi\div14$$

    θ = 41°

    		 use the arc length formula: $$L =\frac{\theta}{360}\times 2\pi r$$, substituting in 10 for L and then solving for θ
    remember: do the opposite to solve the equation, they × you ÷ and vice versa
    so to get rid of all the multiplying, divide 10 by, 2, π  and 14
    to get rid of the over 360, multiply by 360
  • Author
    Posts
Viewing 7 posts - 1 through 7 (of 7 total)
  • You must be logged in to reply to this topic.

maths made easy

copyright © 1995 – 2025

Privacy Policy

ABN: 86 396 190 036

Show Buttons
Hide Buttons
Go to Top