-
Trapezoidal Rule
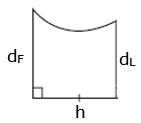
$$A\approx\frac{h}{2}\left\{ {{d_F} + {d_L}} \right\}$$
where h is the height of each subinterval
dF = length of first
dL = length of last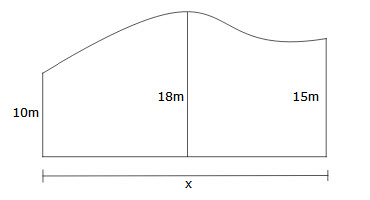
Using Trapezoidal Rule, find the width of this block of land if the area is 776 m2.$$A\approx\frac{h}{2}\left\{ {{d_F} + {d_L}} \right\}$$
$$776\approx\frac{h}{2}\left\{{10 + 18} \right\}+\frac{h}{2}\left\{{18 + 15} \right\}$$
$$776\approx\frac{h}{2}\times 28+\frac{h}{2}\times 33$$
$$776\approx\frac{61h}{2}$$
$$1552\approx61h$$
$$h\approx\frac{1552}{61}$$
$$h\approx25.44$$
hence the width of the field will be 2 × 25.44 (remember: h is the width of each ‘section’, not the entire width)
= 50.88 m
Find the approximate area.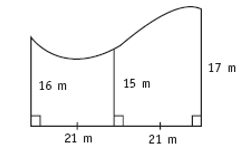 
$$A_1\approx\frac{21}{2}(16+15)$$
A1 ≈ 325.5m2
There are two trapezia here, so we need to find two areas, and then add them
the first area will be the left trapezia
h = 21 dF = 16 dL = 15$$A_2\approx\frac{21}{2}(15+17)$$
A2 ≈ 336m2
the second area will be the right trapezia
h = 21 dF = 15 dL = 17A = 325.5 + 336
= 661.5
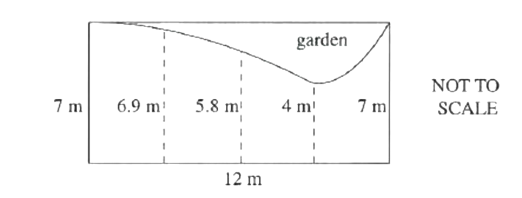Three straight fences and a garden border a piece of land. Find the area of the land by applying the Trapezoidal Rule, correct to the nearest square metre.h = 12 ÷ 4 = 3 step 1: find the height of each section – there are 4 and the entire thing is 12m long so divide 12 by 4 = 3m A1 = 3/2(7 + 6.9) = 20.85m2 step 2: split the area into four parts and find the four areas separately Area 1 has first length 7m, last one is 6.9m A2 = 3/2(6.9 + 5.8) = 19.05m2 Area 2 has first length 6.9m, last one is 5.8m A3 = 3/2(5.8 + 4)= 14.7m2 Area 3 has first length 5.8m, last one is 4m A4 = 3/2(4 + 7)= 16.5m2 Area 4 has first length 4m, last one is 7m A = (20.85 + 19.05 + 14.7 + 16.5)m2
= 71.1 m2
∴ 71 m2Add them together to find the total area
- You must be logged in to reply to this topic.
